基于速度差法超声波流量计的测量原理,分析了硬件延时对测量精度造成的误差。提出可采用二次回波法和声速法来提高测量精度,利用数学模型分析 2 种方法的可行性,最后通过实验验证这 2 种方法,实验结果表明二次回波法和声速法对提高了超声波流量计测量精度的可行性和有效性。
0.引言
速度差法超声波流量计是利用声波在顺流方向与逆流方向的传播速度差来反映流体流速的精密流量计量仪表。其能够实现精确计量的关键在于精确测量声波在顺流方向与逆流方向的传播时间。为提高超声波流量计的测量精度,很多专家学者在各个领域进行了研究,并提出了一系列的改进方法,如峰值检测法、双门限测量法、双阈值比较法、自适应门限触发法、信号质量判断机制等 这些方法提高了超声波流量计的测量精度,也有一些学者通过数学分析及数字算法得到了提 高 超 声 波 流 量 计 精 度 的 方法,但对于速度差法测量中的硬件延时问题尚没有很好的解决方案。本文针对此问题,提出采用二次回波法和声速法 2 种方法,用于提高速度差法超声波流量计的测量精度。
1.速度差法超声波流量计测量原理
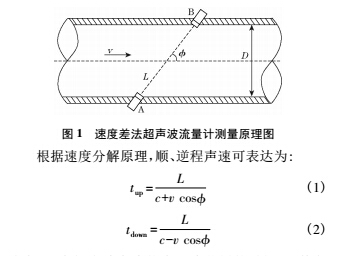
如图 1 所示,速度差法超声波流量计有相对放置的 2 个超声波换能器 A,B,交替发出超声波,超声波发射点与接收点之间的距离为 L,超声波传播路径与流体轴向的夹角为 ,管道截面直径为 D,流体的轴向平均流速为 v。
式中: tup 为超声波在流体中顺流传播的时间,即换能器 A 发射超声波,换能器 B 接收超声波; tdown 为超声波在流体中逆流传播的时间,即换能器 B 发射超声波,换能器 A 接收超声波。

由式( 1) 、式( 2) 可导出超声波信号在顺流方向与逆流方向的速度差公式为
由式( 5) 可知: 管道内径 D、声道角 由超声波管体决定,是一个常数,tup 与 tdown 的测量精度直接影响超声波流量计的测量精度。
2.硬件延时误差分析
超声波流量计的测量原理框图如图 2 所示,由CPU 控制发射驱动电路驱动发射换能器,同时控制CPLD 或专用时间芯片等精密计时电路开始计时接收换能器接收到信号后,CPU 控制信号处理电路对信号进行处理,然后送入计时电路,计时电路计得的时间送入 CPU 进行运算。
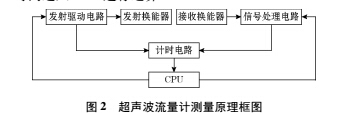
由上述测量原理框图可以看出,流量计通过计时电路测得的时间,不仅包括超声波信号的传播时间 tup
与 tdown ,还包括发射驱动电路的延时、发射换能器的转换延时、接收换能器的转换延时和信号处理电路的延时。若把发射驱动电路的延时、发射换能器的转换延时定义为发射电路的延时,把接收换能器的转换延时和信号处理电路的延时定义为接收电路的延时,计时电路测得时间可表示为
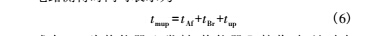
式中: tmup 为换能器 A 发射、换能器 B 接收时,计时电路计得的时间; tAf 为换能器 A 的发射延时; tBr 为换能器 B 的接收延时。
同理,可得: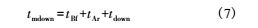
式中: tmdown 为换能器 B 发射、换能器 A 接收时,计时电路计得的时间; tBf 为换能器 B 的发射延时; tAr 为换能器 A 的接收延时。
根据电路结构的不同,换能器的发射延时、接收延时在 50 ~ 500 ns 之间不等,而超声波流量计的顺、逆
器的发射延时、接收延时不做处理,直接将计时电路得到的时间作为超声波传播时间来进行运算,将会引入很大的测量误差,这在流量计进行小流量测量时很明显。同时,由于不同换能器的发射延时、接收延时也不同,如果在零流量时代入计算公式,会造成零点误差。
3.提高测量精确度的方法
由上述分析可知,要提高速度差法超声波流量计的测量精度,必须消除硬件延时误差。本文提出二次回波法和声速法来消除硬件延时误差。
3.1 二次回波法
如图 3 所示,在换能器 A 发射超声波时,换能器 B会接收到 2 个信号,一个是直接接收换能器 A 发射的超声波信号,另一个是换能器 A 发射的超声波由换能器 B,A 两次反射后的信号,可通过计时电路分别计得换能器 A 发射、换能器 B 接收的信号到达时间,和换能器 A 发射、换能器 B 接收 2 次反射后的信号到达时间。
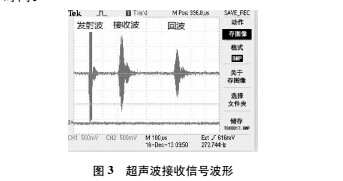
换能器 A 发射、换能器 B 接收的信号到达时间为 tmup ,定义换能器 A 发射、换能器 B 接收 2 次反射后的信号到达时间tmup2 ,这两个时间分别可以用式( 6) 和式( 7) 表示:

在流体静止时,流体流速 v 为 0,tup 与 tdown 相等,分别定义计时电路计得顺程时间为 tmup0 ,2 次反射后的信号到达时间 tmup02 ,由式( 8) 和式( 9) 可计算出硬件延时:
式中: tmdown0 为流体静止时计时电路计得的逆程时间; tmdown02 为换能器 B 发射、换能器 A 接收 2 次反射后的信号到达时间。
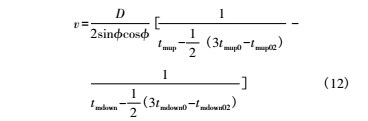
在测量时,用计时电路计得的时间减去硬件延时,即可得到超声波顺、逆程的真实传播时间,由式 ( 5) ~ 式( 7) 可得流体流速公式为采用式( 12) 测量,式中增加了二次回波时间参数,可以实时消除换能器发射、接收的硬件延时,可直接测得超声波在流体中真正的传播时间,从而可精确测得流体的流速值。
3.2 声速法
另一种测量方法是利用测量流体中的声速,在流体静止时计算出流量计的顺、逆程硬件延时,并代入公式参与计算。
在流体静止时,由式( 1) 、式( 4) 、式( 6) 可得顺程
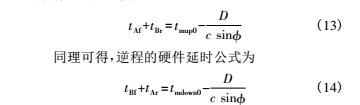
的硬件延时公式为
其中,管道口径 D 与声道夹角 ,在管体加工时已经确定,可以通过实测测得。通过声速测量仪表测得声速参量 c,就可以计算出流量计的硬件延时,在测量过程中减去硬件延时,再由式( 5) ~ 式( 7) 计算,可得流体流速公式为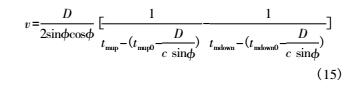
此方法可以通过在流体静止时,使用声速计算得到硬件延时,再代入流速测量公式中参与计算,亦可消除由时间延迟造成的误差。
4.实验验证及分析
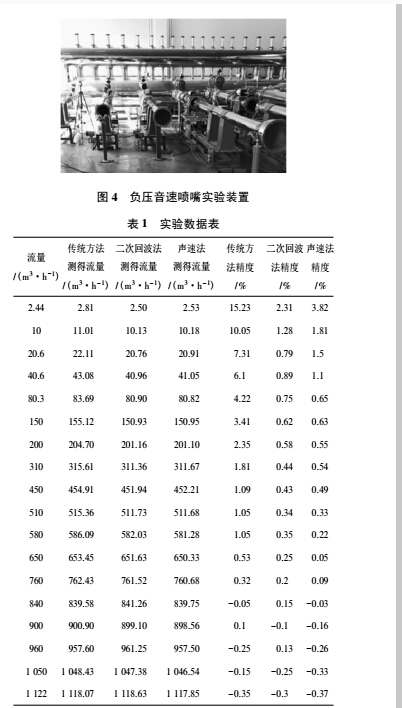
为了验证上述 2 种方法的实际效果,在负压音速喷嘴装置上,如图 4 所示,使用 DN100 口径单声道气体超声波流量计管体进行了实流测试。
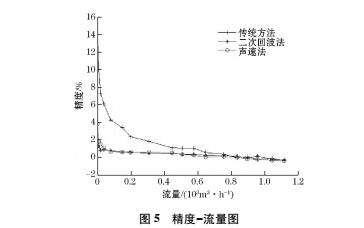
测试过程分别采用了传统理论方法、二次回波法和声速法进行实验,实验数据如表 1 所示,由表中数据绘制精度-流量图如图 5 所示。
由图 5 可知: 传统理论方法获得的精度-流量图线性较差、斜率较大,且在小流量时会产生较大误差;二次回波法和声速法获得的精度- 流量点图线性良好、斜率较小,且在小流量时不会产生较大误差; 二次回波法的精度-流量点图线与声速法的相比,斜率更小,且在同等流量时测量误差更小。由此说明: 二次回波法和声速法均可以大大提高速度差法超声波流量计测量的精度,可直接用于生产实践; 且二次回波法比声速法测量效果更好,其原因是声速法需用其他设备精确测量声速及声道长度,在测量过程中引入了间接误差。
5.结束语
本文针对速度差法超声波流量计计时过程中引入的硬件延时误差影响测量精度问题,分析了误差产生的原因及造成的影响,提出了用二次回波法和声速法来消除硬件延时误差,进而提高测量精度,并通过实验验证了 2 种方法正确性和有效性。其中采用二次回波法更加精确,但测量过程较声速法更加复杂。