针对科氏流量计传感器输出信号的缓变特性，提出了基于希尔伯特（Hilbert）变换的信号处理方法。采用自适应滤波噪声抵消的方法滤除信号噪声，然后利用 Hilbert 变换的相移特性对滤波后的两路增强信号做 Hilbert 变换处理，并与两路 Hil⁃ bert 变换信号做三角组合运算求得相位差，同时构造解析信号解算瞬时频率。结果表明，采用基于希尔伯特方法的信号处理方法实时性高，相位差测量精度在 0.5%以下，频率跟踪速度较基于自适应陷波方法节约近 2 倍的时间，满足计量要求。

科里奥利质量流量计（简称科氏流量计）具有高精度，宽量程以及可测多相流体的优势，是现行流量计中发展最为迅速的流量计之一。当过程流体流过以其固有振动频率（也称作驱动频率）振动的流量管时，由于科里奥利力的作用使得流管两侧产生了与过程流量成正比的相位差。测量传感器捕捉到的相位差以及振动管的固有振动频率，是计算流体质量流量的关键内容。随着数字信号处理技术以及数字信号处理器的发展，研究人员提出一些频率跟踪以及相位差测量的数字处理方法，并逐渐取代了模拟处理科氏流量计信号的方法。

目前科氏流量计信号处理方法主要有：过零检测法 、数字相关法 、离散傅里叶变换 以及希尔伯特变换等相位差测量方法和相位差分法、锁相环方法、小波分析以及自适应陷波滤波 等频率解算方法。国内学者常采用自适应陷波滤波的方法估计信号频率，再用计及负频率的离散时间傅里叶变换 DTFT（Discrete Time Fourier Transform）的方法或者是计及负频率的加滑动窗的 DTFT 方法（简称 SDTFT）来计算相位差。这种方法需要用较长的时间跟踪信号频率，再依据频率进行频谱分析以求相位差，也因此在相位差计算时引入二次误差影响了测量精度。针对该问题，本文提出均采用基于希尔伯特变换的方法处理科氏流量计信号，即同步解算信号的相位差与信号的瞬时频率以避免引入二次误差，提高信号处理实时性。

1.科氏流量计信号模型

科氏流量计左右传感器输出的信号，在理想状态下均为频率、幅值恒定的正弦信号。在测量过程中，由于受到温度、环境噪声、流速和流体密度等的影响，振动管的幅值、频率也会随时间变化，为此徐科军等学者提出了时变信号模型。但在实际应用中，振动管的振动频率更多的是受温度影响，但该影响可以通过相应算法进行补偿，其他情况对频率的影响可忽略不计。因此，本文采用时不变信号模型。在实际测量国内某一型号的科氏流量计时发现，在不同流速情况下，左右传感器输出信号的频率、幅值没有明显变化，但均混有幅值较大的随机噪声。为此，本文采用正弦信号和高斯白噪声的混合信号作为科氏流量计的信号模型，即：

[x(n)= Asin(ω0 n + φ0) + σe(n)] n = 1,2,…,N （1）

其中 N 为科氏流量计信号采样点数，A 为信号幅值，ω0 为信号角频率，φ0 为初始相位，e(n) 为信号噪声，σ 为噪声的幅值范围。

2.希尔伯特信号处理算法与实现

2.1 方法概述及算法原理

传统的基于希尔伯特变换的科氏流量计信号处理方法，均是采用不同结构形式的自适应陷波滤波器，先求解信号的频率，然后对滤波后信号做希尔伯特变换以求取相位差。自适应陷波滤波的方法通过多次的迭代收敛才能估计到信号的频率，给科氏信号的处理增加了较大的计算量，因此本文提出采用基于希尔伯特变换的方法同时计算信号的相位差和频率。

希尔伯特变换器是幅频特性为 1 的全通滤波器，信号通过希尔伯特变换后，其负频率成分作+ 90°相移而正频率成分作-90°相移。因此，当两路正弦信号经过希尔伯特变换后，分别变成幅值相反的余弦信号，再将两组原始信号与希尔伯特变换信号进行三角组合运算可得相位差，同时构造解析信号即可求解信号的瞬时频率，算法原理框图如图 1所示。

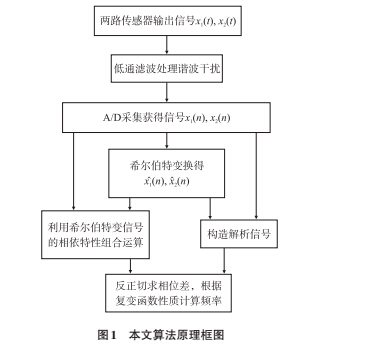
2.2频率解算原理

在实际的信号处理中，直接采集到信号都是实信号的形式，并且大部分属于复分量信号。因此，瞬时频率的解算涉及到复分量信号向单分量信号转换以及实信号向复信号转化两方面的问题。Ville等提出了现在普遍接受的一种瞬时频率的定义，即该信号所对应的解析信号相位函数对时间的导数。利用希尔伯特变换的方法构造解析信号，即实现了实信号向复信号的转化。

给定一实信号 x(t) ，其希尔伯特变换信号为 x̂(t) ，以此来构造解析信号 z(t) ：

2.3 实现过程

科氏流量计传感器理想输出信号为幅值、频率相等以及相位差在 4°以内的两路正弦信号。但在实际采集流量计信号时观察到，信号中会有大量的谐波以及信号噪声干扰。假定滤波后的信号只含信号噪声，设离散后的原两路信号形式如式（1）所示，根据上述算法原理和算法实现框图，其具体的实现过程如下：

第1步：采用基于最小均方算法 LMS（LeastMean Square） 的自适应滤波器对仅混有信号噪声的离散信号进行自适应数字滤波。

基于 LMS 算法 FIR 自适应滤波器具有结构简单，计算量小以及性能稳定的特点，广泛应用在系统辨识、噪声消除和信道均衡等方面。本文主要是对科氏信号做噪声消除，其滤波结构如图 2 所示。

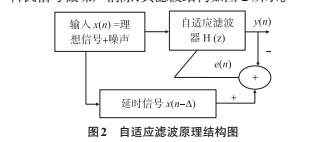
该滤波器利用有源信号间的相关性、噪声的非相关性，使得最小均方误差 e(n) 达到最小值。选择输入信号的延时信号作为期望信号 d（n）以提高与输入信号的相关性，这样更易于提取噪声得到增强信号。通过 LMS 算法不断调整自适应滤波器系数，直到 H（z）收敛到最优解时，y（n）逼近信号噪声，而误差序列 e(n) 逼近信号 x(n) ，达到自适应噪声抵消的目的。

第 2 步 对滤波后的两路信号做希尔伯特变换分别产生 90°相移的希尔伯特变换信号，然后利用两路滤波信号和两路相移信号构造解析信号。产生的两路希尔伯特变换信号为：

对式（7）做反正切运算即可求得相位差 φ 。在介绍瞬时频率解算的的时候，需要对相位函数求导得到信号的瞬时频率，但在做算法处理时，信号均是离散信号，因此在这里采用相邻时间点对应相位的差分作为信号的频率。由计量原理及实现过程可知，基于希伯特变换原理的相位差测量方法无需预知信号的频率，且不受非整周期采样的影响，计算简单并且具有瞬态性。而对于瞬时频率的计算不需要再独立采用过零检测、自适应陷波等传统的频率估计算法，给整个科氏信号处理算法节省了一定的计算量，对于实际测量信号具有广泛的适用性。

3.仿真验证与分析

为验证本文算法的有效性分别做了以下仿真实验：LMS 自适应噪声抵消，噪声对相位差的影响，相位差的动态测量实验，瞬时频率估计的验证实验。本文通过多次测试国内某一型号的科氏流量计得到，此流量计稳定工作时，振动频率大约在 79.5 Hz，参考实验结果模拟出仿真实验信号模型如式（8）所示。

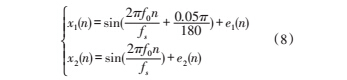
其中，采样频率 fs 为 2 kHz，信号基频 f0 为 80 Hz，信号幅值设为 1，采样数据 N 为 500。

3.1 噪声影响分析

采样信号经过前期的低通滤波处理后，滤波后的信号中依然存在随机噪声，分析了希尔伯特变换方法在不同程度噪声干扰下的相位差测量情况。

信噪比 SNR 设为 0 到 70 dB 的变量值，相位差的理论值设为 0.05°。

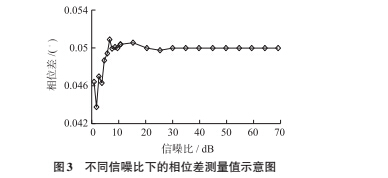
通过多次的独立实验发现，相位差测量值与理论值的偏离程度随着信噪比的增加呈现逐渐减小的一个趋势如图 3 所示。仿真实验表明，信噪比在大于 30 dB 的程度时，相位差测量精度才会较少的受到影响。

3.2相位差动态测量分析

希尔伯特变换可以用于分析瞬时相位差，但从图 3 中也可以看出当信号中有一定的干扰时对于相位差的瞬时分析就会有很大的影响。对于真实的科氏流量计传感器的信号也是会有高频干扰以及系统信号噪声的，因此本文取混有高斯白噪声的信号作为该文算法处理的信号模型。而从图 4 中我们可以观察到，本文相位差测量方法从仿真开始时间点就能很好的跟踪到信号并计算出每一时刻的相位差，表现出了良好的实时性。

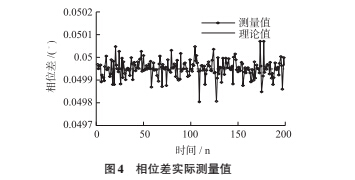
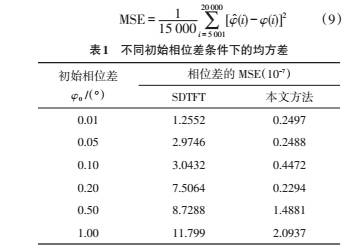
表1 中列出了在不同的初始相位差下，基于文献中 SDTFT 的相位差测量方法与本文提出方法的均方误差 MSE（Mean Square Error）。鉴于两种方法跟踪到信号频率都需要一定的时间，本文求取 5 000 点以后的相位差测量结果与理论值之间的 MSE。从表二可以看出该文方法测得的相位差的 MSE 比基于 SDTFT 方法测得结果降低了近一个数量级。

3.3 瞬时频率估计仿真

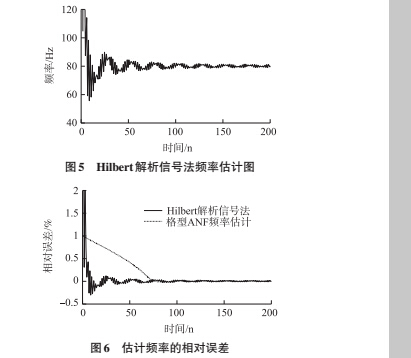
信号本身的噪声以及相位的波动对频率的计算影响较大，采用式（8）所示信号模型，对本文给出的频率估计算法和自适应陷波滤波 ANF（Adaptive Notch Filter）方法进行了计算机仿真对比实验。由于科氏流量计传感器信号会有倍频噪声以及白噪声，这样的条件下使用希尔伯特变换解析信号法求解的瞬时频率是负的，即不正确的。本文提出的频率估计算法是有加入 LMS 滤波算法，进行信号噪声的消除。在信号频率为 80 Hz，采样频率为 2 kHz的条件下，采用 Hilbert 算法进行频率估计，从图 5可以观察到，希尔伯特解析信号法的频率估计方法能够快速并准确地解算出信号频率。与 ANF 频率估计方法相比，计算简单，需要较少的时间就可以检测到信号在每一时间点的频率如图 6 所示。

4.结论

本文提出采用基于希尔伯特变换的解析信号法来处理科氏流量计信号。通过对滤波后的信号进行希尔伯特变换，利用希尔伯特变换的相移特性求得的相位差，具有较高的精度以及良好的动态测量特性，同时构造解析信号计算瞬时频率。结果表明，与传统上采用不同算法结合使用处理科氏信号的方法相比，本文的算法收敛快，计算简单，避免了算法结合使用时的二次误差，提高了算法计算的精度，改善了信号处理的实时性。