涡街流量计是一种朝着高精度、低功耗以及数字化方向发展的广泛应用的流量仪表。 但在低流速下，噪声信号会淹没涡街信号。 因此，如何提高低流速信噪比成为研究热点。 随着 DSP 处理技术的发展，借助于 DSP 强大的数据运行能力和数据处理能力，可将其成功实现。 设计了一套应用小波阈值去噪理论搭建的 DSP 平台，主要设计了信号调理电路。 并通过在该 DSP 平台对不同频率数据进行采集、处理和分析，得出将该研究平台作为涡街信号处理的研究工具是可行的。

目前的涡街流量计普遍采用单片机系统，随着信号处理算法复杂程度的提高，单片机的运行速度和性能已开始成为阻碍涡街流量计性能提升的瓶颈。由于 DSP 处理器具有强大的数据处理能力和快速处理速度，同时 DSP 有较强的硬件和软件支持，使得其对涡街流量计智能设计有着强大的资源支持。 因此，智能仪表控制多采用 DSP 芯片处理器以满足对复杂数据处理的能力。 本文通过所开发的 DSP 研究平台为研究各种复杂算法数字信号处理技术在涡街流量计中的应用提供一种便利的研究工具。

1.涡街流量计信号特点与分析

一台涡街流量计有三个组成部分：涡街产生、涡街信号检测和涡街信号处理。 如图 1。

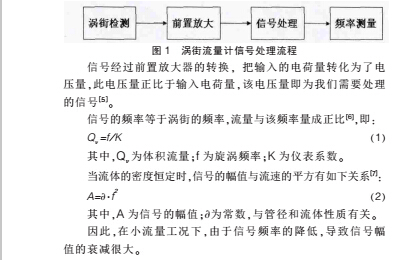
2.DSP 研究平台设计

本系统的研究平台包括信号调理电路，AD 转换电路， 及其与上位机通信接口。

本文主要研究内容是实现应力式涡街流量计信号采集，保存及处理等功能， 这里主要介绍实现将微弱的电荷量转换成与AD 转换器相符合的电压信号的硬件组成电路 ， 即信号调理电路。 信号调理电路包括电荷放大器，低通滤波器，电压放大器和电压偏置电路四部分。

2．1 电荷放大器

应力式传感器采用压电元件，在外力作用下，通过压电元件表面产生电荷来测量非电量。 压电晶体的输出是十分微弱的电荷信号，需经过电荷放大电路，将压电传感器的电荷信号转换为电压量，做为后续信号处理的输入量。 本文在输入级预置一个双端差动电荷放大电路以提高其共模抑制能力。 如图 2。

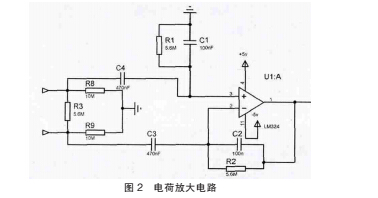
2．2 低通滤波电路

模拟低通滤波电路可以依靠抑制低频信号或者衰减高频信号的电路来滤除所需频带以上的信号，从而提高信噪比，从图 3可以看出，Butterworth 低通滤波电路具有增益较为平坦且线性相位特性良好，因此本文选择 Butterworth 低通滤波电路。

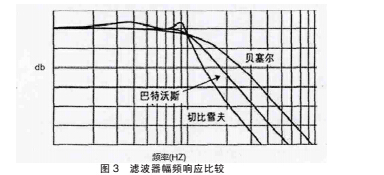
因为本文仅对低流速时涡街信号进行测量， 其频率范围在5～30Hz 内， 所以在设计该滤波器通带衰减－3db， 截止频率为100Hz 时可以满足滤除部分高频噪声的要求。 其中运放采用差动输 入 四 运 算 放 大 器LM324 器件，±5V 电源供电，如图 4 所示。

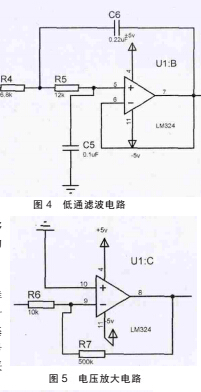
2．3 电压放大电路

由于涡街信号经过电荷放大器转换为电压信号后幅值较小，信号采集精确度太低。往往需要加入电压放大电路对涡街信号提供足够的增益， 以提高信号处理的精度。 电路如图 5 所示。

2．4 电压偏置电路

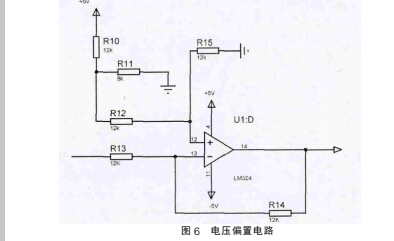
采用的 AD 芯片的采样输入范围为 0～5V，通过设计偏置电路， 在原有信号的基础上加入偏置电压， 使信号调理到适合 AD 采样电路采样的范围，如图 6 所示。

3. 实验研究与结果分析

3．1 实验数据采集

本文通过所设计的 DSP 平台采集频率为 8Hz、15Hz和 30Hz的涡街信号并保存其中，得到三组涡街信号数据，如图 7 所示。

3．2 实验数据处理

根据小波阈值去噪原理，将三组数据分别导入 Matlab 中进行去噪处理，处理结果如图8所示。

分别对去噪后信号进行 FFT 变换，横坐标为频率，纵坐标为幅值，如图 9 所示。

3．3 实验数据分析

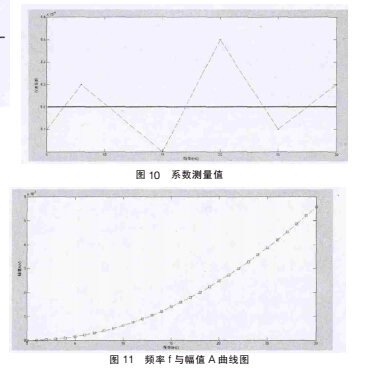
在 A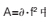＝中，由于鄣的值与仪表系数，管道口径，流体性质等因素有关，不同的应用场合会有不同的数值。 通过对不同流速进行多次采样，计算出不同频率下对应的幅值，绘制出幅频特性曲线，如图 10。 查出不同频率下信号调理电路的放大倍数，得出从压电传感器输出的实际信号幅值，经过多组数据的计算，得出鄣的平均值，为 6．2×10－6。 从而得出幅值 A 与频率 f 曲线，如图 11。

观察 8Hz 涡街信号对应的 FFT 变换的结果，信号中有 6Hz左右的频率信号。 根据幅频关系可知 6Hz 频率实际信号幅值应在 0．22mV 左右， 但是观察 6Hz 频率现在对应的信号幅值为0．3mV， 可以判断此频率为 6Hz 的信号为噪声干扰。 利用此方法，依次排除其他噪声干扰，确定实际信号频率。

根据信号调理电路幅频曲线可知 8Hz、15Hz 和 30Hz 信号在滤波器的通带，此时的信号经过信号调理电路放大 225 倍。根据 FFT 变换后的结果可知实际信号频率 8Hz、15Hz 和 30Hz 去噪后信号幅值分别为 0．1V、0．35V 和 1．2V， 从而得出压电传感器输出信号幅值为 0．44mV、1．56mV 和 5．33mV。 为了得到精确的实际信号频率，取校验频率为 8Hz 的数据为例，其信号幅值为 0．44mV，代入 A＝鄣·f2，得到此时信号频率为 8．452Hz。 同理分析校验信号为 15Hz 和 30Hz 的处理后信号，如表 1 所示。

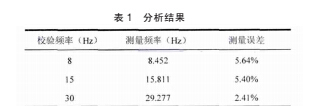
由表 1 的结果可知该分析方法测量误差在可接受范围内，并且随着流速的增加， 信号频率变大， 去噪算法的测量误差变小。 由此可知该 DSP 平台可以应用于涡街流量计的低流速测量信号的去噪分析中。