目前对于涡街流量计的最佳取压位置研究主要集中在二维流场 ，但这不能更生动准确的反映出三维流场特性。采用 Ａｎｓｙｓ＋Ｗｏｒｋｂｅｎｃｈ＋ＦＬＵＥＮＴ 数值仿真软件平台，根据涡街流量计的物理结构尺寸建立仿真模型。并将仿真模型进行网格划分，从而对求解域进行离散，再通过 Ｎ－Ｓ方程进行求解计算，将仿真得到的卡门涡街脱落频率与实验结果比较，得出两者之间的最大误差不超过５．８％，数据表明可以利用ＦＬＵＥＮＴ软件对涡街流量计进行数值仿真。最后利用ＦＬＵＥＮＴ软件，在不同流速下，通过设置多个检测点，对各点信号强度和频谱分布进行比较分析，得出目前最常用的三角柱旋涡发生体的最佳取压位置位于管道中轴线，距离发生体尾部１．４ｄ（ｄ 为旋涡发生体截流面的宽度）的位置处。

1.引言

计算流体力学于1993年初次应用于二维黏性流体偏微分方程。CFD作为一门相对新兴的技术，对实验研究和理论分析方面有举足轻重的作用。它的基本原理是用有限个离散点的变量值的集合来替换原先在时间域或空间域上连续物理量的场，这些离散点上的场变量存在一定关系，根据一定的原则建立代数方程组，便可求出方程组场变量近似值。

ＦＬＵＥＮＴ软件运用ＣＦＤ软件群的思想，具有许多优化的物理模型，广泛应用于流体力学研究中。ＦＬＵＥＮＴ以很直观的观察到流场的实时变化，通过仿真结果来指导物理实验，再由实验结果优化传感器结构，提升开发效率。

目前关于涡街流量计柱体绕流的数值模拟研究，主要集中在二维平面  而在三维特性的数值研究中相对较少。通过对二维涡街流场中的压力场进行数值仿真研究，解释了信号强度随检测位置变化的原因。通过非定常ＲＮＧｋ－ε模型对圆柱绕流、方柱绕流和绕立方柱流动进行了仿真研究，得出钝体绕流的非定常流动能够采用非定常雷诺平均法进行研究，且实验结果优于定常模拟方法的结果。通过对圆柱发生体流场进行数值仿真实验，揭示了影响探头位置的各种因素以及发生体下游尾迹区域对涡形成以及脱落的影响。通过对二维单圆柱绕流进行数值模拟研究分析，得出圆柱绕流的流动与Ｒｅ数的大小有关，

本文选取了应力式涡街流量计进行研究，它提取涡街频率的原理是通过信号处理单元提取涡街流量计旋涡发生体上的压电敏感元件产生的电信号，从而依据流体流量与涡街频率的关系得出被测流量。在以往的涡街流量计设计中，一直将研究重点放在真实流场分析中，即软硬件的设计上。由于在现场管道环境下进行测试实验时，需要重复更换口径、调节流量，操作起来费时费力。所以欲采用涡街流场数值分析的方法对传感器内部流场的变化进行研究，通过仿真结果来指导物理实验，并根据物理实验结果进一步完善传感器结构。。

最后通过ＦＬＵＥＮＴ软件建立三维模型对涡街流量计流场进行仿真 再和气体流量装置上的实验数据进行对比验证 研究表明涡街流量计传感器的研究采用ＦＬＵＥＮＴ数值仿真是有效的。并通过设置多个检测点，在不同流速下对其进行取压，最终得出三角柱旋涡发生体的最佳取压位置在距离发生体尾部１．４ｄｄ（ 为旋涡发生体截流面的宽度）处的管道中轴线处。

2.涡街流量计原理

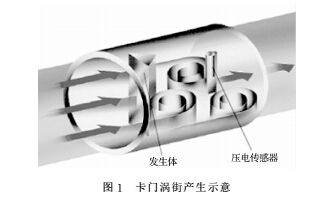
涡街流量计利用流体振动进行流量测量，基本原理是将非流线型旋涡发生体放置在和被测介质流向垂直的方向，当该发生体有流体流过时，在发生体后方两侧交替地分离释放出两列规则的交错排列的旋涡，即为卡门涡街，如图１所示。

旋涡脱落频率f与发生体两侧平均流速V1之间存在如下关系：

F=Ｓｔｖ１/ｄ                          (1)

式中：Ｓｔ为斯特劳哈尔数；d为旋涡发生体宽度。

3.涡街流场模拟的可行性

3.1几何模型的建立和网格划分

本 文 提 出 利 用ＡＮＳＹＳ Ｗｏｒｋｂｅｎｃｈ－Ｇｅｏｍｅｔｒｙ和ＡＮＳＹＳＷｏｒｋｂｅｎｃｈ－Ｍｅｓｈ作为ＦＬＵＥＮＴ 的前处理，并将导出的网格文件直接导入ＦＬＵＥＮＴ 中进行计算。

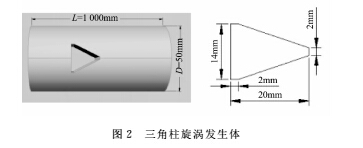
图２是在Ｇｅｏｍｅｔｒｙ中建立的三维几何模型，管道口径D为50mm;管道长L为1000mm;旋涡发生体截流面宽度ｄ为１４ｍｍ.

通过ＡＮＳＹＳＷｏｒｋｂｅｎｃｈ－Ｍｅｓｈ对几何模型划分网格,并将发生体周围网格细划，如图３所示。然而在旋涡发生体壁面附近薄层中的黏性力作用下，顺着壁面法线方向存在较大的速度梯度，因此在网格划分中设置边界层，网格划分所采用的网格单元为ＱｕａｄＴｒｉ／ ，即扫掠网格区域中只包含四边形和三角形单元。

3.2仿真参数的设置

3.3仿真结果与实验结果的误差分析

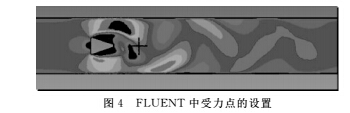
涡街流量计通过压电晶体检测发生体后的压力变化，得到旋涡脱落频率。在 ＦＬＵＥＮＴ 后处理软件 ＣＦＤ－Ｐｏｓｔ中，以相同的原理对涡街流量计进行流场仿真。在旋涡发生体后设置一个检测点（图4十字形标记位置），然后记录该点所受静压力的变化趋势，从而得出旋涡脱落的频率，最后将此结果与实验结果相比较。

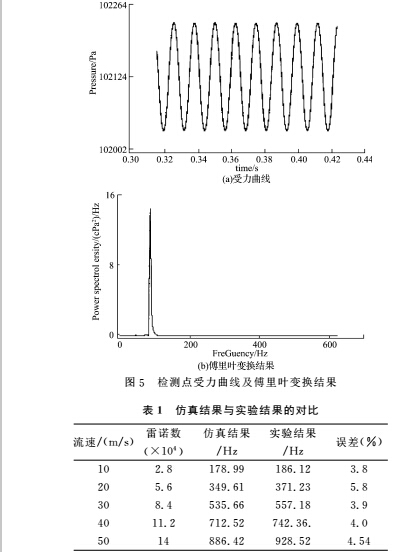
由图５（ａ）可以看出该点所受静压力以一定的时间周期变化，因此可以采用傅里叶变换，得到涡街的脱落频率，如图５（ｂ）所示。为了与仿真结果进行比较，设置实验条件与仿真条件基本一致。在管径为 ５０ｍｍ，流体介质为空气，旋涡发生体为三角柱形的压电式涡街流量装置上进行了实验。比较仿真数据与实验数据，得出最大误差为５．８％（此误差是由实验中发生体尺寸不精确或是发生体插入位置有偏差引起），如表１所示。

4.最佳取压位置的仿真结果

基于前文对ＦＬＵＥＮＴ 三维流场仿真的可行性研究，本节应用ＦＬＵＥＮＴ对涡街流量计检测点的最佳取压位置进行了研究。

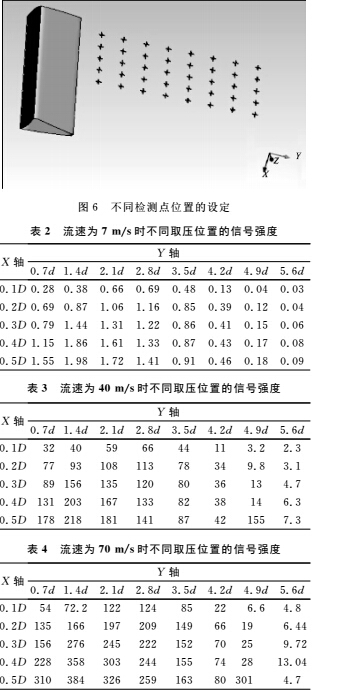
在距旋涡发生体尾部，第１步：以 Ｘ 轴方向０．１Ｄ（Ｄ为管道直径）为步长从管壁至管道轴线位置生成纵向点；第２步：以Ｙ 轴方向０．７ｄ（ｄ 为旋涡发生体截流面的宽度）为步长重复步骤一。最终生成４０个检测点（见图６），并观察这些点上的旋涡信号强度。最后通过数值仿真，将记录的每个检测点的压力变化的时域信号进行傅里叶变换，得到了在７ｍ／ｓ、４０ｍ／ｓ和７０ｍ／ｓ流速下不同检测点的信号强度，如表２～４所示。

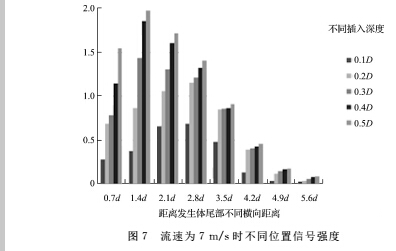
将表２的数据绘制成图７。图７可以直观的反应出各个位置上的信号强度变化。由图７可以看出，信号强度会随着取压位置的不同而不同。当插入深度相同（如０．１Ｄ 时），距离发生体尾部不同横向距离的信号强度近似于正态分布，其中在１．４ｄ的时候达到了峰值，原因是旋涡脱落要经历一个成长－强壮－衰减的过程；当距离尾部的横向距离保持不变（如０．７ｄ时），增加插入深度，发生体尾部的信号强度逐渐增强，其中在管道中轴线位置信号强度最强。

通过对比表２～４中不同流速下的仿真实验数据，得出结论：

１）涡街的信号强度与流速成正比，所以随着流速的增加，旋涡脱落频率信号强度会显著增加。

２）压电探头在逐渐远离旋涡发生体的过程中，涡街信号幅值先逐渐变大，然后又逐渐变小，并且随着流速的增大，这种趋势越来越明显。

５.结 论

本文通过模拟涡街流量计三角柱绕流现象，研究其对附近流场的影响，并将仿真结果与实验结果进行误差分析，可以得出仿真结果与实验结果十分相近，验证了ＦＬＵＥＮＴ数值仿真用于涡街流量计的三维流场是可行的。在涡街流场的仿真中，通过在ＦＬＵＥＮＴ 中设置不同检测点并将结果进行计算处理，对比分析不同流速下各个取压位置的信号强度，找到了涡街流量计的最佳取压位置，并且对计算的结果有了更深层次的了解。这对以后的实验起到指导性意义。

进一步的研究可以在以下方面展开：修改旋涡发生体的形状、尺寸；修改数值模拟方法；修改介质条件。