针对浮子流量计非线性校正中常用的分段线性拟合和最小二乘法不足 ，以及最小二乘支持向量机参数难确定问题，提出了一种基于人类学习优化－最小二乘支持向量机算法（HLO－LSSVM）的仪表非线性校正方法。 首先简介了最小二乘支持向量机和人类学习优化算法，接着阐述了 HLO－LSSVM 算法进行非线性校正的实现过程，分别采用分段线性拟合、最小二乘法和 HLO－LSSVM 算法对浮子流量计非线性校正问题进行了对比。 结果表明，HLO－LSSVM 算法具有更优的校正效果，实现简单，具有良好的应用前景。

浮子流量计引是以浮子在垂直锥形管中随着流量变化而升降，改变它们之间的流通面积来进行测量的体积流量仪表。 磁阻式金属管浮子流量计由磁阻传感器、外部感应磁钢、内嵌磁钢的浮子和金属管道组成。 流量计输出的流量值与浮子位移 h 成正比。 由于磁阻式浮子流量计在测量过程中受到温度、 磁场的影响，其输出浮子位移 h 与磁阻传感器输入 v 的关系为非线性。 克服传感器非线性的传统方法包括了硬件补偿法、最小二乘法和分段线性拟合法。 这些传统方法复杂、需要样本多，精度低，且当更换新的流量计，必须再次进行复杂的计算，可操作性差。

本文提出了一种 HLO－LSSVM 算法的非线性校正方法，利用人类学习优化算法（HLO）对最小二乘支持向量机（LSSVM）的参数进行优化方法，用于解决浮子流量计的非线性校正问题。

1.基于 LSSVM 的流量计非线性校正

磁阻式浮子流量计的磁阻材料的阻值会随外部磁场变化而变化。 复杂的工作现场可能会存在较强的外部磁场干扰。 同时磁阻材料阻值也会随环境温度的变化而变化， 所以流量计输出浮子位移 h 与磁阻传感器输入 v 的特性总是存在一定的非线性。从理论上较难推出浮子位移与流量计输出的函数关系。 浮子流量计输出浮子位移 h 与磁阻传感器输出 v 可以由式（1）表示：

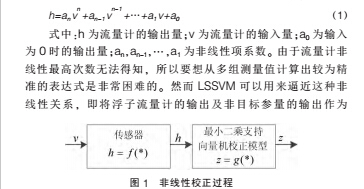
径向基函数的核宽度参数 δ2 体现了训练样本数据集的分布特性，能够确定局部邻域的宽度。 较大的 δ2 意味着较低的方差。 最小二乘支持向量机表达式的正则化参数 γ 用来调节LSSVM 置信范围和经验风险的比例 ， 取折中以使泛化能力最好。 这两个参数的变化对最小二乘支持向量机的校正结果有很大的影响，对这两个参数的选取决定了线性拟合的好坏。 因此，寻找最优参数将是提高 LSSVM 性能的关键。

2.基于 HLO－LSSVM 的流量计非线性校正

人类学习优化算法 （Human Learning Optimization Al-gorithm，HLO）是由 Wang 等人于 2014 年提出的一种模拟人类学习机制启发式算法，利用群体智能搜索较好的解。 该算法收速度快，设置参数少、算法简单易实现等优点，已在多个应用问题上表现出优势。

文采用人类学习优化算法优化选取 LSSVM 参数及其核函数参数。 人类学习优化算法模拟人类的学习过程，人类学习过程可以看作是一个迭代的优化过程：人们通过不断地学习，掌握和提高技能，就像优化算法迭代地寻找最优解。 人类学习优化算法采用的是二进制编码，每一位比特代表人类学习优化算法中解决问题知识的一个组成成分。该算法通过随机学习、个人学习和社会学习操作算子来求解优化问题。 其迭代公式如式（9）。

其中，i＝1，2…M，M 是种群规模的大小，i 表示第 i 个个体；j表示个体的第 j 维；xij 表示个体 i 在第 j 维的知识；rand（0，1）表示等概率地生成 0 或者 1；ikij 代表第 i 个个体的历史最优解（个体最优）的第 j 维的值。 skj 表示所有个体的历史最优解（全局最优）中

第 j 维的值。 rand()表示［0～1］ 之间的随机数 ； pr 表示随机学习的概率；pi 表示个体学习的概率。

所有个体完成学习后， 新解的适应度值通过适应度函数计算获得。 若新适应度值比上一个个体最优解优， 则更新此解，否则不更新；

全局最优解以同样的方 式更新。 HLO＿LSSVM实现过程如图 2 所示。

3.浮子流量计非线性校正实例

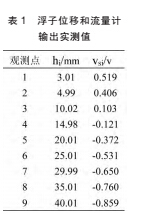
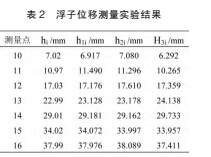
本文通过实验测得 16 组浮子位移 hi 与磁阻传感器输出 vsi 的实测值。 其中 9 组用来进行非线性校正训练，如表 1 的 hi 所示。 剩下的 7 组用来进行验证对比，如表 2 的 hi 所示。

3．1 HLO＿LSSVM 校正结果

在 Matlab 2014a 软件中，本文分别采用 HLO－LSSVM 算法、分段线 性 拟 合 算 法  （Piecewise  LinearFitting，PLF） 和最小二乘法拟合算法（Least Square Method，LSM拟对表 1 中数据进行了非线性校正。

HLO－LSSVM 算法的参数设置如下所示。 种群规模为 10，迭代次数为 30，随机学习概率 Pr＝0．2，个体学习 概 率  Pi ＝0．93，  正 则 参 数  γ ＝467．859，径向基函数参数 δ2＝1．312

算法优化和非线性校正

结果与分段线性拟合和最小二乘法对比结果如表 2 所示。 其中，hi 表示浮子实测高度，h1i 表示

HLO－LSSVM 测量的浮子高度，h2i 表示分段线性拟合测量的浮子高度，

h3i 表示最小二乘法拟合测量的浮子高度。

3．2 结果对比

为了更好地分析出实验结果，本论文采用和方差（SSE）和

均方差（MSE）评价拟合效果。

其中，n 是数据的个数，hi 是原始数据，hi 是预测的数据。

HLO－LSSVM 算法的方差 表 3 对比结果

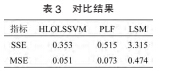
和均方差均小于分段线性拟合和最小二乘法拟合的和方差和均方差，说明人类学习优化算法

最小二乘支持向量机具有更好的拟合效果。