讨论了电磁流量计矩形和鞍状线圈所产生磁感应强度的分布情况。运用毕奥萨伐尔定律和叠加原理，通过数值仿真得到励磁线圈在测量管道内电极横截面上的磁场分布情况。提出磁感应强度的方向平行程度和大小均匀程度２个指标，并用其来判别感应磁场分布的均匀程度。依据以上２个指标，分别对不同尺寸的矩形和鞍状励磁线圈所产生的感应磁场进行计算分析和优化。

１.引 言

电磁流量计结构简单，其内部无活动部件和阻流元件，具有可靠性高、精度高的特点，目前在冶金、石油化工、医疗、农业灌溉、城市给排水等领域都有广泛应用。电磁流量计是利用法拉第电磁感应原理测量导电液体体积流量的仪表 ，励磁线圈安装在测量管道的外部，产生垂直于测量管中心轴线的感应磁场Ｂ，当导电性液体通过电磁流量计时切割磁力线，传感器检测电极上会产生正比于流体流速Ｖ的感应电动势Ｅ。通常可表达为：E=KBDV,其中ｋ为仪表系数，Ｄ为测量管道内径。

流速Ｖ之间的关系为：Ｑ＝π/4D平方V,因此Q=（πD/4KB）E0

故当磁感应强度Ｂ与管道内径Ｄ一定时，流量Ｑ仅与流体中产生的感应电动势Ｅ成正比，而与其它物理参数变化无关。上述公式只是简单地说明电磁流量计的工作原理，只有满足一定的条件时才能成立 ：（１）在无限大范围内，磁感应强度Ｂ呈均匀分布；（２）流体速度如同固体导体一样，其内部质点的速度处处相等，与平均流速相同。

 励磁线圈的结构决定了电磁流量计感应磁场的分布特性，线圈和感应磁场的研究对提高电磁流量计性能具有重要意义。张小章 用理想化磁场模型对大管径多电极电磁流量计磁场进行计算研究。

ＭｉｃｈａｌｓｋｉＡ等 利用有限元方法建立电磁流量计励磁线圈的３Ｄ混合数学模型。金宁德等 采用有限元方法计算四电极电磁流量计磁场分布特性，并分析仪器偏心及流体磁导率变化因素对磁场分布特性影响。李斌等 给出计算矩形鞍状线圈在测量管内磁场分布的一种折线近似算法。徐立军等 采用有限元方法，对不同轴向长度线圈所产生激励磁场的平行程度作分析。黄安贻等 在非均匀磁场电磁流量计基础上，求解励磁线圈的截面形状，并仿真线圈的磁场。邬惠峰等 利用有限元方法建立电磁流量计传感器场路耦合模型，以提高励磁系统的研究效率。滕涛等 从磁偶极子的磁场理论出发，对外流式电磁流量计和油管构成的环形空间中磁场分布情况进行数值仿真。对用于明渠测量的电磁流量计，文献分析了鞍状和双甲板形状线圈的磁场分布均匀程度以及磁场边界效应。傅新等 介绍了一种基于测量边界条件的分区解析式磁场重构方法，并用于电磁速度探针附近磁场的重构。

为获得分布均匀的磁场，本文对电磁流量计矩形和鞍状励磁线圈的磁场分布特性进行数值分析，提出判别磁场分布均匀程度的指标，考察励磁线圈的形状、尺寸等因素对磁场分布特性影响，为电磁流量计励磁线圈优化设计提供研究方法。

２.电磁流量计感应磁场计算与仿真

根据毕奥萨伐尔定律，载流导线上电流元Ｉｄｌ在点Ｐ处产生的磁感应强度ｄＢ为：

根据式（３）对电磁流量计励磁线圈所产生感应磁场分布情况进行数值计算与仿真。以２个励磁线圈几何中心连线为ｘ轴，２个电极所在直线为ｙ轴，测量管中心轴线为ｚ轴，建立空间直角坐标系。在该坐标系下，计算励磁线圈在测量管道内电极横截面上产生的感应磁场，其步骤如下：（１）在ｘ ｙ平面上测量管道的电极横截面内，对２个线圈之间区域进行网格化，并确定每一网格点对应的坐标值（ｘ，ｙ，０），网格划分越细，区域内磁感应强度计算精度越高；（２）把载流导线划分成微电流元的集合，并确定每一微电流元矢量ｄｌ的坐标（ｌ，ｌ，ｌ）；（３）计算从ｘ ｙ ｚ每个网格点到电流元的径矢ｒ（ｒ，ｒ，ｒ）及其距离ｒ；ｘ ｙ ｚ（４）在区域内每个网格点处，分别计算第ｔ个电流元产生的磁场强度矢量在ｘ、ｙ方向上的分量Ｂｘ和

３.感应磁场均匀程度指标

由于流体运动平行于ｚ轴，磁感应强度沿ｚ轴方向的分量对电磁流量计检测电极的感应电势信号没有影响，所以可忽略此分量，此时励磁线圈在测量管道内电极横截面上产生的磁感应强度可表示为：Ｂ＝

Ｂｘｉ＋Ｂｙｊ。因此在所考虑电极横截面上，每点处磁感

４.矩形与鞍状线圈感应磁场优化

４．１ 矩形线圈感应磁场的仿真及优化

对于矩形线圈，将所考虑横截面区域划分成４１×４１个网格，令矩形线圈的宽为 ６ｃｍ，等于管道内径２Ｒ。每个励磁线圈的匝数为６，厚度为２ｃｍ，２个线圈之间的距离为６ｃｍ，紧贴测量管壁，线圈中电流强度为１０ｍＡ。首先令矩形线圈轴向长度的范围从Ｒ到８Ｒ，间隔为Ｒ；其次，在前面所确定最优尺寸４Ｒ附近，提高尺度分辨率，从 ３Ｒ到 ５Ｒ，间隔为０．２Ｒ。考查矩形线圈在测量管横截面上的感应磁场分布情况，如表１所示。

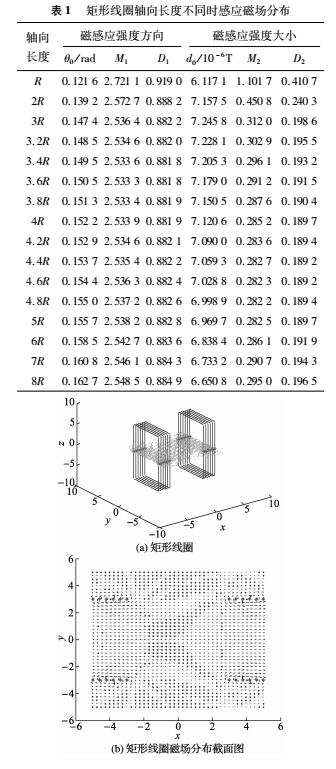
由表１可知，当矩形线圈的轴向长度为４．４Ｒ时，Ｄ２达到最小，Ｄｌ取值０．８８２２与最小值０．８８１８相差不大，表明此时磁感应强度分布更为均匀。此时矩形线圈在测量管内电极横截面上的感应磁场分布情况如图１所示，图中的点为励磁线圈与电极横截面的交点。

４．２ 鞍状线圈磁场的仿真及优化

对于鞍状线圈，把电极横截面区域划分成４１×４１个网格，鞍状线圈的轴向长度为 ６ｃｍ。每个励磁线圈的匝数为６，厚度为２ｃｍ，线圈紧贴测量管壁，线圈中电流强度为１０ｍＡ。首先令线圈圆弧段的弧度范围为９０°～１８０°，间隔１０°；其次，在前面确定最优弧度１６０°附近，提高尺度分辨率，从１５０°到１７０°，间隔２°。鞍状线圈在电极横截面上的感应磁场分布情况，如表２所示。

由表２可知，当鞍状线圈圆弧段的弧度为１５４°时，Ｄ２达到最小值，Ｄ１ 取值 ０．９７４４，同时感应磁场方向指标 θ为０．０９５４，与最小值０．０９１１相差不大，综合考虑选鞍状线圈圆弧段的最优弧度为１５４°。

取鞍状线圈圆弧段的弧度为１５４°，首先取线圈的轴向长度范围Ｒ～６Ｒ，间隔为Ｒ；其次在最优尺寸２Ｒ附近，提高尺度分辨率，从 Ｒ到 ３Ｒ，间隔为０．２Ｒ。

考查鞍状线圈在电极横截面上的感应磁场分布情况，如表３所示。

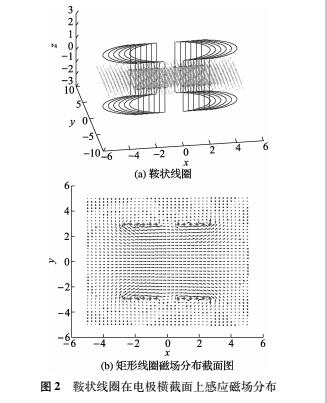
由表３可知，当鞍状线圈的轴向长度为１．４Ｒ时，Ｄ 达到最小，Ｄ 取值０．８３６９，磁场方向指标 θ取值０．１２５２。表明鞍状线圈轴向长度为１．４Ｒ、圆弧段的弧度为１５４°时，其感应磁场分布更为均匀。此时鞍状线圈在测量管内电极横截面上的磁场分布情况如图２所示。

５.矩形与鞍状线圈磁场对比分析

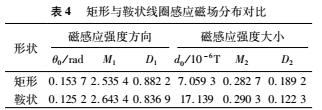
依据以上２个磁场均匀度指标，对优化后的矩形和鞍状线圈，在电极横截面上的磁场分布情况进行对比，如表４所示。

由表４可知，从磁感应强度方向和大小２个方面，鞍状线圈较矩形线圈整体分布更均匀；同时鞍状线圈可提供的感应磁场也更强。此时矩形和鞍状线圈磁场强度方向的具体分布情况分别如图３和图４所示，磁感应强度大小的具体分布情况分别如图５和图６所示。

对比图３和图４，也可以略微反映出鞍状励磁线圈较矩形励磁线圈磁感应强度方向整体平行程度更好，与表４中的结果一致。

对比图５和图６，也可看出鞍状励磁线圈较矩形励磁线圈磁场强度大小整体均匀程度更好，与表４中的结果一致。

６.结 论

 为获得分布均匀的感应磁场，在传感器测量管道内电极横截面上，对矩形和鞍状线圈产生的感应磁场分布进行数值计算和仿真。提出了判别磁感应强度矢量分布均匀程度的２个指标：磁感应强度方向平行程度和大小均匀程度。依据２个表示感应磁场均匀程度的指标，对不同尺寸下的矩形和鞍状线圈的感应磁场分布情况进行分析比较。结果表明：经过优化设计后，相比矩形线圈，鞍状线圈产生的感应磁场分布更为均匀，同时可提供的感应磁场更强。本研究电磁流量计不同形状、尺寸励磁线圈产生的磁场分布特性，对励磁线圈的优化设计具有参考意义。