将有限元理论与可靠性设计理论相结合，利用 ＡＮＳＹＳ提供的 ＰＤＳ概率设计模块进行 Ｖ 锥流量计的参数化建模，编制 ＡＰＤＬ命令流，建立 Ｖ 锥流量计结构的可靠性分析文件，为 Ｖ 锥流量计结构优化提供了理论依据。

0.引言

在管道中进行流量测量的众多方法中，V 锥流量计与其他流量计相比，如孔板式、经典文丘里管式、环形 孔板式等流量计具有以下明 显优势。：较强的自整流功能，所以对于流量计的前直管段要求较短，可以实现在较小的空间内进行安装；由于 Ｖ 锥流量计内的锥形结构的存在及其测量原理的独特性，使得流量计的节流装置抗污染能力强；由于在测量过程中具有较宽量程比，因此它的测量线性度好，测量精度较高；测量过程中，流量计前后之间的压差小，故压损小，因此可以降低能耗；安装简便，易于维护，在长期使用过程中维护费用相对较低； 锥流量计是一体式结构，并无可动部件，从而 Ｖ 锥流量计在使用过程中具有很好的重复性。但是，由于 Ｖ 锥流量计特殊结构，要求锥型节流装置必须通过Ｌ型悬臂支撑的方式固定在管道内，这就使得流量计在长期使用过程中因承受流体载荷的作用，出现锥型节流装置脱落等现象，造成了 Ｖ 锥流量计结构可靠度的下降，严重影响到流量计正常的使用。因此，Ｖ 锥流量计的可靠度研究成为一个亟待解决的问题。

文中利用蒙特卡洛数值模拟法对 Ｖ 锥流量计的可靠度进行分析，用概率统计的方法定量考虑了实际存在的种种不确定性因素，因而，能够更加客观地反映出 Ｖ 锥流量计在实际使用中的可靠性问题。通过对模拟结果的分析可以直接观察出随机变量对于 Ｖ 锥流量计可靠度的影响情况。

1.蒙特卡洛法的原理

蒙特卡洛法（ＭｏｎｔｅＣａｒｌｏＳｉｍｕｌａｔｉｏｎ）以数理统计理论作为基础，利用计算机技术作为辅助手段来实现对于随机变量进行的数值计算的方法，因此，蒙特卡洛法又被称之为随机数值模拟法。Ｍｏｎｔｅ－Ｃａｒｌｏ法应用到流量计可靠性分析的基本原理是：根据 Ｖ 锥流量计的自身结构及其在使用环境中的外在条件，建立一个如下的状态函数：

Ｆ＝ｇ（Ｘ１，Ｘ２，…，Ｘｐ） （１）

式中：Ｆ———结构状态函数；

Ｘ１，Ｘ２，…，Ｘｐ ———影响状态函数的 ｐ 个随机变量。

将上述ｐ 个随机变量代入到状态函数中，进行验算得到该变量在状态函数中产生的一个随机数。通过这个方法，将ｐ 个随机变量代入到状态函数中得到一个分别与之相对应的一个随机数（共有ｐ 个）。在这ｐ 个随机数中，假设其中有ｑ个小于１（根据安全系数法的定义，将随机数小于１的定义为失效，通过安全系数表示 Ｖ 锥流量计的安全状态），当在模拟过程中产生的随机数样本总数足够多时，根据数理统计原理中的大数定律可以知道，此时的实验计算的频率就会接近于实际应用的概率，因此，可以得到 Ｖ 锥流量计的破坏概率为：

ｐ

ｐｆ ＝

ｑ

可靠度为：

ｐｒ ＝１－ｐｆ

2.结构可靠性理论

机械结构的可靠性理论是将随机方法理论如概率论、数理统计知识与随机过程相结合并应用到机械产品的设计与分析中，目的是研究设计产品失效概率或者追踪当前产品的使用可靠度。产品设计过程中，对于结构可靠性产生影响的因素有很多，这些因素都表现出不同程度的非确定性，即为随机性，将这些影响因素根据影响程度进行划分，将主要因素定义为设计时的随机变量进行可靠性分析。应用可靠性理论把设计中涉及到的一组变量处理成一系列随机的变量，并假设他们都服从一定的概率分布（分布类型已知）。这些随机变量之间的关系可以通过概率函数的方法进行数值变换，得到与之相对应的应力 －强度的概率干涉模型。应力 －强度干涉理论是进行机械结构可靠性分析的理论基础。

3.Ｖ锥流量计的可靠性计算

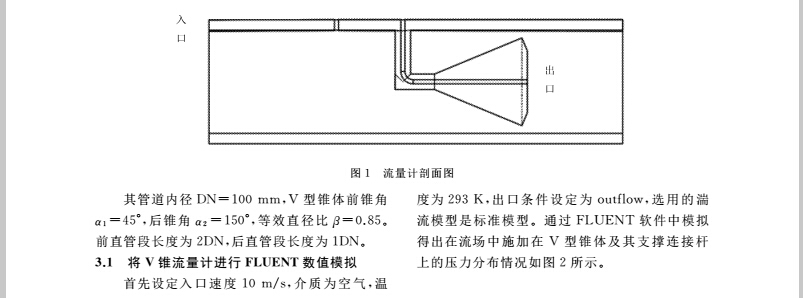
Ｖ 锥流量计节流装置与管道的剖面视图如图

1所示。

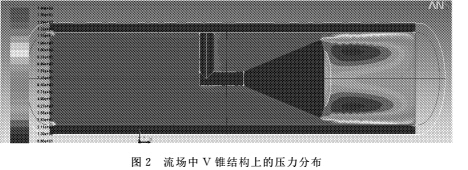
３．２ 在ＰＤＳ模块中进行蒙特卡洛法模拟

３．２．１ 确定设计随机变量并初始化对 Ｖ 锥流量计结构有影响的设计变量作为参变量，并赋予初始值。本例中取锥体的横杆Ｌ、直径为ｒ、杆的半径Ｒ、压力值 ＰＲＥＳＵＲＥ、密度

ＤＥＮＳＩＴＹ、杨氏模量 ＹＯＵＮＧ 作为随机变量。

３．２．２ 参数化建模、网格划分、加载并求解通过具体的设计尺寸及其相关随机变量进行建模。可以建立节流装置的三维立体图，但这样的迭代过程中对于计算机的要求过高，使得计算效率很低。为了提高计算机的计算速度，进行

ＡＰＤＬ建模时，略去次要因素，只保留节流装置即锥体和Ｌ 支撑连杆，然后进行划分网格，在竖直连杆的上端施加固定约束及依据流场分析情况在装置的表面上施加压力载荷，进行求解。

３．２．３ 提取相关的参数结果并存储到参数中由于 Ｖ 锥流量计的主要失效形式是锥型节流装置掉落，最大应力ＳＭＡＸ的值大于或者接近材料强度值，所以出现破坏。因此，利用＊ＧＥＴ命令提取整体结构中的最大应力值ＳＭＡＸ，并将其保存到参数表中作为概率分析时的输出变量。

３．２．４ 生成概率设计的分析文件将上述的 ＡＰＤＬ 命令整理后生成进行一个

概率设计时所需要分析文件，即格式为＊ＭＡＣ形式的宏文件。

３．２．５ 运行概率设计确定输入的随机变量Ｌ、ｒ、Ｒ、ＰＲＥＳＵＲＥ、

ＤＥＮＳＩＴＹ、ＹＯＵＮＧ及其分布；确定输出随机变量为ＳＭＡＸ、ＵＭＡＸ，选择蒙特卡洛法中提供的拉丁超立方模型。执行概率设计，设定分析循环次数为１００次。

３．２．６ 数据分析根据 ＡＮＳＹＳ软件中 ＰＤＳ模块的运行结果

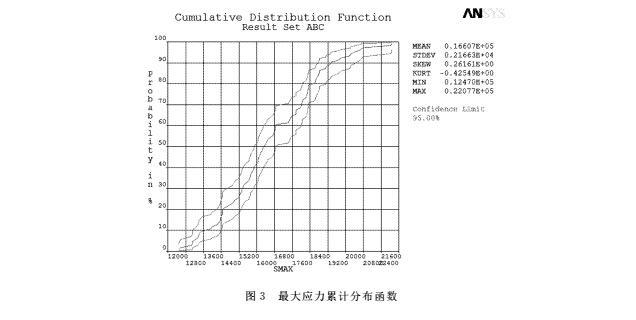
进行提取，得到 Ｖ 锥流量计的可靠度值。在置信水平为９５％ 的条件下节流装置的可靠度约为９５．８８２％。同时，可靠度的大小还与抽样的次数有关，抽样次数越多，得到的可靠度就越精确。最大应力的累积分布函数如图３所示。

4.结 语

通过利用 ＡＮＳＹＳ软件中的ＰＤＳ模块，并编写 ＡＰＤＬ命令流的分析文件对 Ｖ 锥流量计的可靠性进行设计，不仅可以大大提高结构设计的效率，同时也为复杂结构（复杂的系统）的可靠性分析提供了新的解决思路。因此，将ＰＤＳ引入到可靠性结构设计中具有一定的实用意义。