振动信号参数估计是科氏流量计振动控制和流量解算的基础。针对科氏流量计振动信号特征，基于最小二乘与函数逼近原理，提出一种适用于科氏流量计振动信号的参数估计方法。该方法利用FFT 粗估计出信号频率，据此设定频率搜索区间，解最小二乘方程获得信号余弦幅度、正弦幅度和直流偏移，改变频率逐次逼近真值，使得误差平方和最小，最小误差平方和所对应参数即为参数估计值。仿真分析了估计精度和抗噪性能，对F200S 型科氏流量计实测信号进行了参数分析与估计，结果表明了该方法估计的准确性和实用性。

1.引言

科里奥利质量流量计（简称科氏流量计）具有测量精度高、可测流体范围广以及多参数测量等一系列优点，受到广泛关注。科氏流量计在驱动电路作用下，维持其测量管以稳定幅值和固有频率简谐振动，通过检测振动信号频率和相位差，解算出流体质量流量。振动信号参数估计是流量解算和振动控制的基础。

针对科氏流量计振动信号的参数估计，国内外研究者开展了较多研究，提出了频率估计的 DFT 法、CZT法、ANF 法等和相位差估计的过零检测法、互相关、滑动Goerztel 法、Hilbert 变换法[8]、计及负频率影响的滑动DTFT 法等。这些方法主要集中在频率和相位差估计。随着科氏流量计向数字化发展与其应用范围的不断推广，需要更为详细地估计科氏流量计信号频率、幅值、相位和直流偏移的参数特性。

本文提出一种科氏流量计振动信号参数的最小二乘估计方法，通过频率逐次逼近和求解最小二乘方程获得信号频率、幅值、相位和直流偏移的估计值，将讨论方法估计精度和抗噪性能，并对罗斯蒙特F200S 型流量计振动信号进行估计，验证方法的有效性。

2.科氏流量计振动信号

2.1振动方程

在激振器电磁力驱动下，科氏流量计充液测量管振动看作刚体以一定角速度 ω 的旋转运动。根据刚体转动定理可得测量管振动微分方程：

振动稳定后，在驱动力作用下阻尼振动被抵消。科氏流量计驱动频率理应与测量管固有频率吻合，使得振幅最大，即 ω = ω0 ，则科氏流量计振动信号方程为：

y(t) = ym cos(ωt + φ) （3）

式中，初相 φ = π/2 ，振幅 ym = Mdm /ξω0 。可见，科氏流量

计信号近似正弦波形。

2.2信号描述

根据式（3）所示科氏流量计振动信号方程，考虑实际信号中存在直流偏移，用式（4）描述科氏流量计信号。

y(t) = A cos(ωt) + B sin(ωt) + C（4）

其中，余弦幅度 A = sin(φ) ，正弦幅度 B = cos(φ) ，C 为直流偏移，ω 为信号频率。 A B C 和 ω 为需要估计的科氏流量计信号参数。

3.参数估计的最小二乘法

3.1方法原理

设科氏流量计信号在 tk (k = 0 1 N - 1) 时刻的采样值为 x(k) ，于是

y(k) = A cos(ωtk ) + B sin(ωtk ) + C（5）

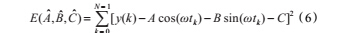
若已知信号频率 ω = ω0 ，设余弦幅度、正弦幅度和直流偏移的估计值分别为  B̂ Ĉ，于是信号参数估计值与真实值之间的误差平方和：

由于需要估计的参数有4 个，信号频率 ω 亦是待估计量，最小二乘法不能直接计算出结果。此时，可通过函数逼近实现4 参数估计。

3.2方法流程

首先利用FFT 对信号频率进行粗估计，根据频率粗估计值，利用上述最小二次原理计算出余弦幅度、正弦幅度、直流偏移以及估计误差平方和，然后改变频率，重复上述操作，在得到的一系列估计误差平方和中找出最小的一组，其对应的信号频率、余弦幅度、正弦幅度和直流偏移，即是科氏流量计振动信号参数估计值。方法流程如图1 所示。

3.3实现步骤

具体实现步骤如下：

步骤 1 利用 FFT 粗估计出信号频率 ω0 ，令频率搜

索区间 [ωl ωh] =[ω0 ± ωc /N ] ，其中 ωc 为时钟频率，N 为参与FFT 的数据长度，设 Dῶ= ωh - ωl 。

步骤 2 设 i 为计算次数，从区间 [ωil ωih] 中等间隔取 2M + 1 点，若 i = 1，则[ω1l,ω1h] =[ω0 ± ωc /N ]，利用式（6）~式（8）分别计算出这些点对应的余弦幅度 Aij ，正弦幅度 Bij ，直流偏移 Cji 与误差平方和 Eji ，j = 1 2 2M + 1 。

步骤3 比较 Eji ，找出最小误差平方和 min(Eji) 及其对应的信号频率 ωi 、余弦幅度 Ai 、正弦幅度 Bi 和直流偏移 Ci ，其中，频率估计的最大偏差为 Dω = Dῶ/M i 。

步骤4 调整计算次数和频率搜索区间，令 i = i + 1 ，ωil = ωi - 1 - Dῶ/M i - 1 ，ωil = ωi - 1 + Dῶ/M i - 1 。

步骤5 重复步骤2~步骤4，直到搜索出满足精度要求的信号频率，同时记录其他对应的余弦幅度、正弦幅度和直流偏移，即实现信号参数估计。

由实现步骤可知，本文方法较FFT 法增加了解最小二乘方程进行频率搜索的过程，因此运算量有所增加。具体运算量与频率分辨率及搜索区间长度要求有关，要求的分辨率越高，运算量越大。通常依FFT 粗估计确定的搜索区间较短，搜索次数较少，可基本满足工程应用。

4.仿真分析

仿真实验中，以含噪声正弦信号作为信号源，信号频率 f = 100 Hz ，余弦幅度 A = 0.3 mV ，正弦幅度 B =0.4 mV，直流偏移 C = 0.05 mV，即信号幅度 ym = 0.5 mV，信号相位 φ = 0.643 5 。所加噪声为均值为0 的高斯白噪声，信噪比 SNR = 10 。采样频率 fs = 2 000 Hz，采样序列长度 N = 1 024 。

4.1估计精度

利用 FFT 和本文方法估计信号频率、直流偏移、振幅和相位，重复100 次，求出相对误差的均方根值（Rootof Mean Square，RMS）。表1 给出了一组参数估计值和RMS。从表中可以看出，FFT 法和本文方法均可实现信号参数估计，但FFT 法因受非整周期截断和频谱泄漏影响，频率误差最大可达0.5 个分辨率，相位误差最大可达 π/2 ，而本文方法不受非整周期截断影响。

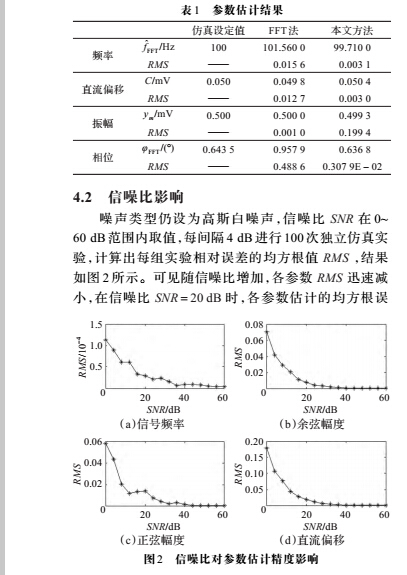
差 RMSf  = 0.329 2 ´ 10-4，RMSB = 0.633 6 ´ 10-2，RMSA =0.698 9 ´ 10-2 ，RMSC = 1.759 8 ´ 10-2 。科氏流量计实际信号受噪声干扰较小，信噪比较高，本文方法能满足实际应用需要。

5.实测信号参数估计

在数字化油库实验室，实际采集F200S 型（配1700 型变送器）科氏流量计mV 信号。实验环境为平稳水流量，采集装置使用NI USB9234 多通道数据采集器，采样频率设为20 kHz。取水流量稳定在102.5 kg/min 时采集的mV 信号，分析科氏流量计信号波形和频率。由图 3（a）所示信号波形可知科氏流量计信号近似正弦信号，幅值约为0.3 V，表2 给出了信号参数。用汉宁窗截取 1 024 个采样点，利用FFT 估计出信号频率为195.31 Hz，其频谱如图3（b）所示。

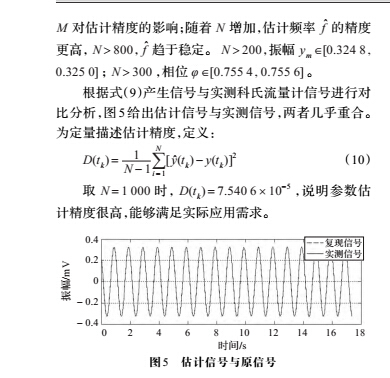
M 对估计精度的影响；随着 N 增加，估计频率 f̂的精度更高，N > 800，f̂趋于稳定。 N > 200，振幅 ym Î[0.324 8 0.325 0] ；N > 300 ，相位 φ Î[0.755 4 0.755 6] 。

根据式（9）产生信号与实测科氏流量计信号进行对比分析，图5 给出估计信号与实测信号，两者几乎重合。为定量描述估计精度，定义：

6.结束语

针对科氏流量计振动信号特征，基于最小二乘原理提出了一种振动信号参数估计方法，给出了方法原理、方法流程和实现步骤。仿真分析了方法精度与信噪比影响，对实际采集F200S 型科氏流量计振动信号进行了参数估计，结果表明利用本文方法估计的参数可产生与科氏流量计信号几乎一致的复现信号，均方误差 D(tk ) = 7.540 6 ´ 10-5 ，说明了本文方法的有效性、准确性。