针对传统 FMECA 对故障模式危害性分析主观化、经验化的缺点，应用模糊数学方法定量化传统定性评价指标。以燃油流量计为例，建立因素集、评价集，采用层次分析法确定因素权重、隶属函数法确定模糊评价矩阵，给出基于模糊理论的燃油流量计各故障模式的危害度等级，并与风险优先数法( ＲPN) 比较，表明前者具有较大优势。通过二级评判计算燃油流量计故障对发动机控制系统的危害度等级，结果对发动机控制系统的可靠性设计和验证有较大意义。

引言

燃油计量系统是发动机控制系统的重要组成模块，其主要功能是根据发动机内部的电子控制器( En-gine Electronic Control Unit，EECU) 向燃油计量系统提供燃油度量信号，由燃油流量计计算出燃油喷嘴需喷出的相应流量，并将流量信号返回至 EECU。因此燃油流量计的可靠性是影响发动机控制性能、甚至飞机的飞行安全的重要因素，对燃油流量计的可靠性分析尤为重要。

故障模式、影响与危害性分析 ( Failure Modes， Effect and Criticality Analysis，FMECA) 方法广泛应用于硬件可靠性分析。但在分析过程中常出现模糊性语义和不确定性的概念，同时相关故障统计数据的缺乏也使得定量分析难度增加。为解决上述问题，本文在传统 FMECA 的基础上，运用模糊数学理论进行改进，并以燃油流量计为例开展分析。

1.燃油流量计的传统 FMECA

燃油流量计根据 EECU 传递的相关信号，计量燃油喷嘴喷出的燃油流量，从而控制发动机的转速。其功能原理如图 1 所示。

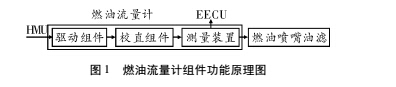
燃油从液压机械组件 ( Hydro Mechanical Unit，HMU) 流出，首先进入燃油流量传感器的驱动组件，驱动测量部件旋转，再经过校直装置去除燃油中的漩涡和其他扰乱，进入测量装置，通过测量装置中的叶轮、鼓状筒、传感线圈得到燃油流量信号，提供到 EECU。流出燃油流入燃油喷嘴油滤过滤，去除燃油中的杂质。表1给出了燃油流量计的 FMEA 结果。

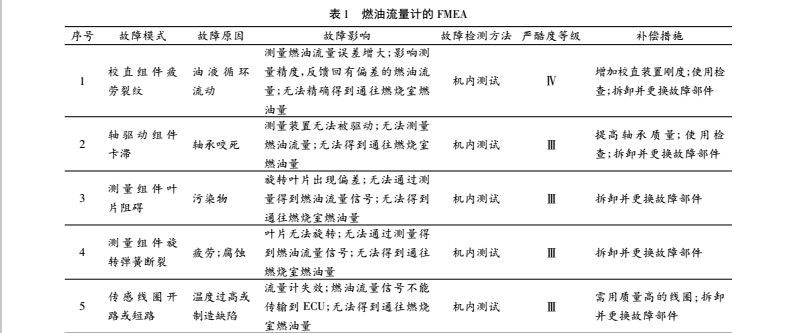
对燃油流量计的危害性分析( Criticality Analysis，CA) 采用风险优先数( Ｒisk Priority Number，ＲPN) 。选择严酷度( S) 、故障发生概率( O) 和检测难易程度( D）作为评判因素，获得燃油流量计的危害性分析结果如表2.

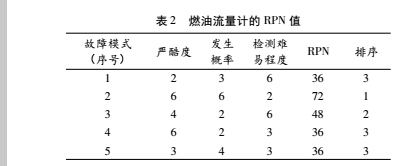
从表 2 中可以看出，在几个主要故障中，有 3 个故障的风险优先数 ( ＲPN) 数值相同，暴露了使用传统

FMECA 方法评价故障模式危害性的弊端。同时依赖评分人的经验对三个评判因素进行打分存在较大的主观性和不确定性。为了解决这些问题，本文将层次分

析法、隶属函数法等模糊数学理论应用到燃油流量计的 FMECA 中，以获得一种更为合理的排序。

2.燃油流量计的模糊 FMECA

2． 1  模糊 FMECA 方法

以二级模糊综合评判为例来说明模糊 FMECA 方法的一般步骤

1) 确定评价集并分配权重。

确定评价因素集合 U = { u1 ，u2 ，…，ui ，…} 和评价等级标准集合 V = { v1 ，v2 ，…，vj ，…} 。其中 ui ( i = 1，2，…，n) 是需要评价的因素。vj ( j = 1，2，…，m) 是对于每个因素需要评价的等级。本文采用层次分析法 对各因素分配权重，描述各个因素对评价的影响作用大小。权重的指标 W = ［w1 ，w2 ，…，wn ］，0 ＜ wi ＜ 1 满足归一m化条件 ∑wi  = 1 。

2) 进行一级模糊综合评判确定模糊评判

矩阵的方法主要有统计法和隶属函数法。前者由专家打分得出最终模糊判据矩阵，但由于系统的复杂性和专家经验的有限性，虽然此方法简单易行，但具有一定的误差，结果也带有一定的主观性，故本文采取隶属函数法，得到各故障模式的评判矩阵:

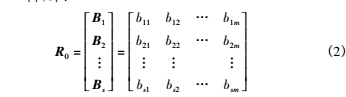
所以，综合考虑二级指标的权重因素 W0 = ［w1 ， w2 ，…，wn ］，可以得到二级模糊综合评价的结果为 B = W0 Ｒ0 =［b1 ，b2 ，…，bm ］。

对于层次更多的情况，可以将前一级的评价结果作为评价矩阵，采用相同的方法评价。

2． 2 故障模式 1 的模糊 FMECA

1) 确定因素集

通过对燃油流量计实际的调查和分析，对燃油流量计进行故障危害性评价时，评价因素集为 U = { 发生概率，严酷度，检测难易程度} 。

2) 确定评价集

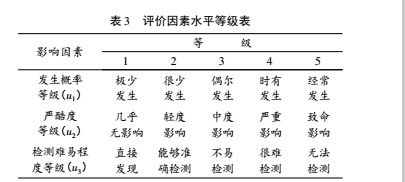
将因素水平分为 5 个等级: V = { 1，2，3，4，5} 。不同影响因素的划分标准，根据表 3。

3) 建立故障模式 1 的模糊评价矩阵

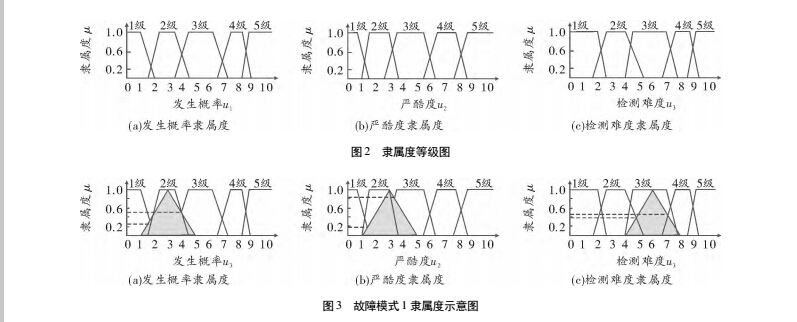
本文采用隶属函数法得到模糊评判矩阵。对于五等级的评价集，航空工业对发生概率、严酷度、检测难度三因素普遍采用的隶属度图 如图 2。

其中，横坐标为对应因素模糊评定等级大小，从 0 到 10 等级依次增加，一般给出一个范围，纵坐标为隶属度大小。根据表 1，给出燃油流量计各故障模式各因素模糊评定范围，如表 3、表 4 所示。

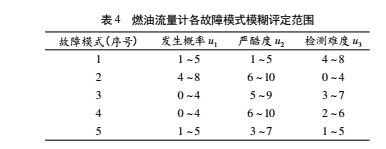
对于故障模式 1，其发生概率 u1 范围为 1 ～ 5，在图 2 ( a) 中以( 1，0) ，(3，1) ，(5，0) 为顶点画出三角形，如图 3

( a) 所示。

三角形与各个等级交点的纵坐标，构成故障模式 1 发生概率隶属度模糊评价集为 Ｒ11 = ［0． 33，1． 00，0． 51，0． 00，0． 00］。

根据表 4，故障模式 1 的严酷度 u2 和检测难易程度 u3 范围为 1 ～ 5 和 4 ～ 8，相应在图 2 ( b) 、( c) 中以 ( 1，0) ，(3，1) ，(5，0) 和以( 4，0) ，(6，1) ，(8，0) 为顶点画出三角形，如图 3( b) 、( c) ，得到故障模式 1 严酷度 u2 隶属度模糊评价集为 Ｒ12 =［0． 18，1． 00，0． 83，0． 00，0． 00］，检测难易程度 u3 隶属度模糊评价集为 Ｒ13 =

的可靠性设计和验证。

3.结束语

燃油流量计的模糊 FMECA 分析结果表明在燃油流量计各故障模式中，轴驱动组件卡滞导致测量装置无法被驱动( 故障模式 2) 的危害等级最高，其次是测量组件旋转弹簧断裂导致叶片无法旋转( 故障模式 4) 和测量组件叶片阻碍( 故障模式 3) 。传感线圈( 故障模式 5) 和校直组件( 故障模式 1) 故障危害性相对较小。因此在开展燃油流量计可靠性设计和改进工作时，应把重点放在轴驱动组件和测量组件上，此分析结果与实际基本符合，表明该方法具有一定的应用价值。

在传统的危害性分析时，采用风险优先数方法得到故障模式 1、4、5 的 ＲPN 值相同，不能对这三种故障模式的危害度进一步比较，而模糊 FMECA 则解决了此类问题。同时模糊 FMECA 方法应用模糊数学理论将严重程度、故障发生概率、检测难易程度等定性指标定量化，使可靠性分析结果更加科学、合理、准确。