采用经验模态分解（EMD）方法对涡街信号中混杂的干扰噪声进行滤除，提取出真实的涡街信号。 该方法首先将原始信号输至二阶低通滤波器进行幅值归一化，然后将处理后的信号经 EMD 算法分解成各噪声分量和真实涡街信号分量，进一步通过施密特阈值翻转法统计频率并且判别出真实的涡街信号所在的分量，从而达到提取涡街信号的目的。最后，通过对在线涡街流量信号进行仿真分析，验证了该数字信号处理方法的有效性。

涡街流量计的理想输出是周期的正弦信号。 但在实际应用中，当流量很小时，涡街传感器输出的信号比较微弱，易被噪声淹没，存在一个下限死区，从而造成量程比受限。 另一方面，来自探头及管壁的震动也会对涡街信号产生极强的干扰。 中低频涡街信号的处理问题是制约涡街流量计发展的主要问题。

针对上述问题， 国内外专家学者及世界著名仪表公司运用不同的信号处理方法对涡街流量信号进行处理。 这些方法对涡街信号的幅值信息均没有做最大化的利用， 在噪声强度超过一定上限后，均存在方法失效的风险。本文通过对 EMD 的研究，提出了一种全新的方法解决高强度噪声的问题。 在线仿真实验表明，该方法具有很好的滤波性能。

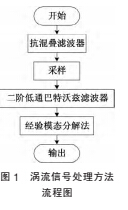
1.信号处理系统方案设计

文设计的信号处理系统主要采用 EMD 算法进行涡街信号的提取。 EMD 算法可以将信号分解成不同稳态分量，但无法自动识别哪一阶分量为有效涡街信号。 因此本文提出利用信号的幅值阈值来分辨真实涡街信号所在分量。

本文首先将原始涡街信号输入至一个二阶低通巴特沃兹滤波器进行滤波：一方面可以滤除其中的高频信号；另一方面，该二阶滤波器可使原始信号幅值归一，方便后续信号处理。

接着将幅值归一化的涡街信号通过经验模态分解方法进行分解，滤除干扰信号，得出真实涡街信号。 该系统的信号处理流程图如图 1所示：

1．1 二阶低通巴特沃兹滤波器

文献指出， 涡街信号的幅值与频率存在平方关系。 另外由于实际涡街信号混杂着各种各样的噪声，因此涡街信号的幅值随频率的不同有很大的变化。 信号处理时很难制定统一的幅值标准来进行滤波。

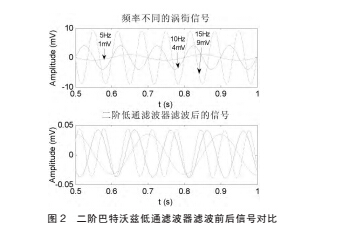
本文算法中， 二阶低通巴特沃兹滤波器采用 IIR 数字滤波的形式，将有效频率量程内的信号幅值进行－40dB ／ dec 的衰减。 很好的平衡了涡街信号幅值随频率平方递增的关系。 达到各频率点幅值归一化的效果。 如图 2 所示，涡街信号 A＝0．04f2（mV），取 5Hz、10Hz、15Hz 三个信号，经转折频率 fc＝1Hz 的二阶巴特沃兹低通滤波器滤波后，输出幅值均为 0．04mV。

1．2 EMD 分解

EMD 分解可将一个复杂的信号分解成若干个稳态 IMF 分量之和，每个 IMF 必须满足两个条件：

条件 1：在整个数据段内，极值点的个数和过零点的个数必须相等或相差最多不能超过一个；

条件 2：在任意时刻，由局部极大值点形成的上包络线和由局部极小值点形成的下包络线的平均值为零，即上、下包络线相对于时间轴局部对称。

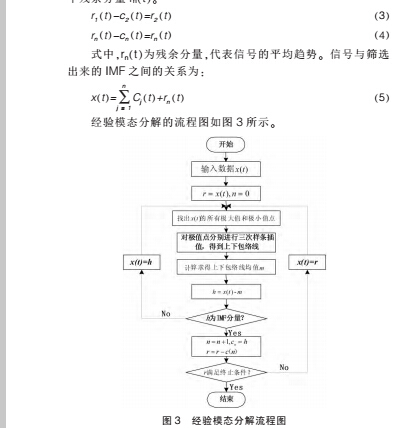
采用以下步骤对信号 x（t）进行 EMD 分解。

1）先确定信号所有的局部极值点 ，然后用三次样条插值函数去拟合，形成信号的上下包络，计算上下包络的均值 m1（t）。

2）令 h1（t）＝x（t）－m1（t），理想的是 h1（t）满足 IMF 的条件时将 h1（t）记为 c1（t）。

3）一般情况下 h1（t）是不满足 IMF 条件的 ，就将 h1（t）当做是原始信号来处理，重复上述步骤。 先得到上下包络线的平均值m11（t），再去判断 h11（t）＝h1（t）－m1（t）是否满足 IMF 的条件，直到h1k（t）满足 IMF 的条件为止，记 c1（t）＝h1k（t）。

4）将 c1（t）从 x（t）中分离出来，令 r1（t）＝x（t）－c1（t）。 将 r1（t）又当做原始数据，重复上述步骤，按照相同的方法筛选出其他满足条件的 IMF 分量，直到不能满足筛选条件为止，这时只剩下一个残余分量 rn（t）。

2.系统信号处理仿真实验

本文设计的信号处理方法采用实验室自主研发的涡街流量计硬件平台采集涡街数据，将在线实验数据输入至 MATLAB 软件进行数据处理。 现场环境：液体，50mm 口径，强 50Hz 干扰情况，一定程度老化的高温探头，流量频率 f＝14．16Hz。 其中无干扰情况下拟合得到的涡街信号幅值 A＝0．021f2。

2．1 二阶低通滤波器滤波

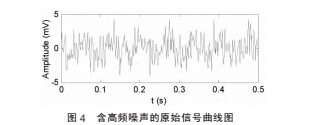
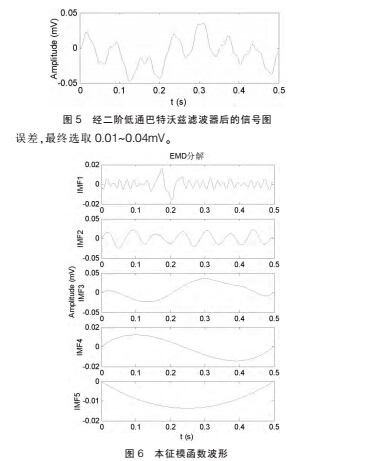
本文采用 fc＝1Hz 的二阶低通滤波器进行滤波。 图 4、图 5 分别为原始信号曲线图及经二阶低通巴特沃兹滤波器后的信号曲线图。

滤波后，理论的涡街信号输出幅值应为 0．021mV。图 5 可以看出，除真实涡街信号外还有其他噪声，

2．2 EMD 分解

按照前文介绍的 EMD 分解法对图 5 信号进一步分解，可以得到该信号的 5 个本征模函数曲线，如图 6 所示。

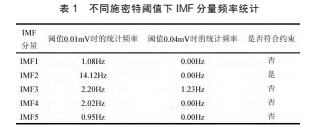
对于有效幅值的选取，应以 0．021mV 为基准，考虑到测量误差，最终选取 0．01～0．04mV。

将图 6 中 5 个本征模函数分别用 0．01mV 和 0．04mV 为阈值的施密特触发器进行翻转并统计频率。 统计方法采用算数平均法。 结果如表 1：

涡街信号有效量程为 2Hz～140Hz。  阈值为 0．04mV 时，IMF3 有频率测出，说明该分量幅值过大，可做为干扰排除。 阈值为 0．01mV 时，IMF2、IMF4、IMF5 均有频率测出， 涡街有效信号的选取基于量程范围内，最大 IMF 分量频率的原则，即 IMF2。

图 7 为该信号 FFT 频谱分析。 可以看出，在强 50Hz 干扰环境下， 运用本文提出的方法所得出的 IMF2 所测频率与 FFT 频

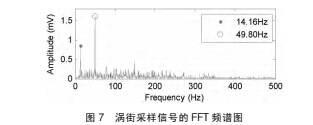
 率误差仅为 0．3％。

2．3 EMD 方法的不足

一般情况，EMD 方法均可以很好的完成涡街信号的提取，但因为 EMD 方法是对时域信号的稳态分量进行提取，若噪声本身是非稳态的，则强制分解成稳态后，可能会对 IMF 分量有很强的污染。 例如图 6，IMF1 中 0．2s 处并不能完美提取 50Hz 分量。因此，若要对 EMD 方法完美使用，仍需进一步改进前期去除非稳态噪声的滤波方法。

3.结束语

EMD 算法提取的信号是各模态的平稳信号，只要有流量存在，必将有一模态代表纯净的涡街信号。 因此，只需利用涡街信号与频率平方成正比这一关系，对各模态的幅值进行筛选，即可达到滤波目的。 本文应用 MATLAB 软件对在线数据进行分析，结果表明，该信号处理方法具有较强的滤除噪声的能力，算法误差小于 0．3％。