介绍了 Gauss-Jacobi 积分方法在超声流量计中的应用，并针对目前多声道超声流量计流量数值积分方法无法满足非理想流场下测量性能的要求，提出了基于实际管路流态分布的数值积分优化方法。通过单弯头理论模型、实流实验分别进行了验证。单弯头理论模型优化后，使超声流量计测量误差最大值由 0． 380% 降低到 0． 056% ; 实流实验结果优化后，中高流速点的测量精度也提高了 3． 60% 左右。

随着能源和水资源的全球性匮乏，一批关系国计民生的大型水利工程和引水调水工程在我国迅速发展，如三峡水利枢纽及南水北调工程等。这些工程项目中经常包含一些口径和流量都很巨大的管道，如水电站机组进水管道等，常规流量计无法适应。近年开发的多声道超声流量计较好地解决了大口径水流量测量的技术难题，流量计制造不受管道口径的限制，多声道配置可以适应较为复杂的流道结构和流态分布，故超声流量计已成为大口径水流量测量的最佳技术选择 。

超声流量计在计算管道流量时所采用的数学模型的准确度对整个测量精度有着非常重要的意义。目前普遍使用的平行布置多声道超声流量计用 Gauss-Jacobi 积分方法来计算管道体积流量，其各声道高度和权重系数的确定都是针对理想的充分发展管道流动，而在非理想管道条件下，如果继续采用相同的数值积分方法会造成非理想管道流动引入的附加不确定度。

针对这一问题，国内外学者也进行了深入的研究。但是前人对此课题的研究均是在理想流场中对理想流动进行积分方法的改进，笔者基于非理想管路的流态分布来对数值积分方法进行优化研究，并选取了工业现场常见的单弯头流场作为研究对象，通过单弯头理论模型和实流实验分别进行验证，从而提高了超声流量计的测量精度。

1.数值积分方法优化

1.1 Gauss-Jacobi 积分方法

超声流量计利用超声波在流体中传播的时间存在差异的特性 由置于待测截面两侧的一对换能器测量超声波顺流与逆流传播的时间 td，i、tu，i，得到相应声道上的平均轴向速度( 简称声道速度) ，其原理如图 1 所示。

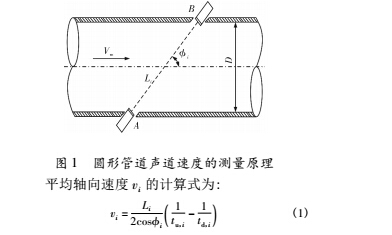
式中 i ———声道数号，i= 1，…，N;

Li———声道长度;

N———声道数，此处取 N = 4;

—i——声道角。

为了提高流量计的测量准确度，在待测截面上平行地布置多条声道，获得的声道速度可以代表待测截面上相应平行条带内的平均速度，如图2 所示，图中 zi 为声道高度，li = Li sin i 为声道宽度，并依据各声道所占的权重系数 ωi ，用加权求和的方法计算流量。

2.优化积分方法的验证

以下将从速度分布的理论模型和实流实验两方面分别验证优化积分方法的有效性。笔者选取了工业现场常见的单弯头流场作为研究对象。为便于处理数据，定义了相对误差:

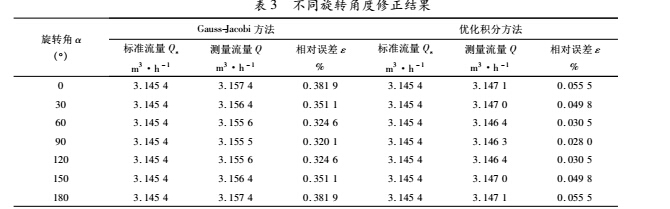
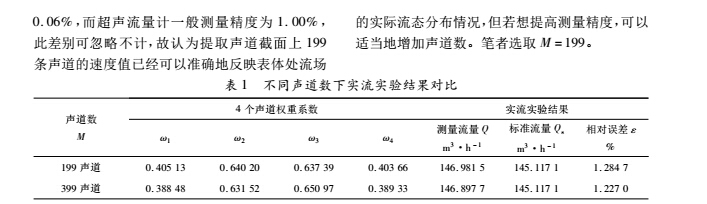
由表 3 可以清晰地看出，在不同旋转角下，优化后，相对误差得到明显改善，Gauss-Jacobi 方法的相对误差在 0． 32% ～ 0． 39% 之间; 而优化的数值积分方法的相对误差最大为旋转角为 0°时，误差只有 0． 055 5% 。

2． 2 单弯头实流实验

鉴于理想 Salami 模型，与实际安装管路单弯头下游流场有差别，为验证实际流场中优化的数值积分方法的有效性，开展了单弯头实流实验。

本实流实验使用的是独立加工设计的四声道超声流量计，其声道位置按照 Gauss-Jacobi 方法中的声道位置进行布置。实验依托于天津市过程参数检测与控制重点实验室的水流量标准装置，采用标准表法对超声流量计进行测量，实验管径D 为 100mm，水流量标准装置精度可达 0． 05% 。

超声流量计前后直管段长度均为 10D，为了尽量消除单弯头上游阻流件( 弯头及蝶阀等) 对流场的影响，在单弯头上游设置了约 30D 的直管段。

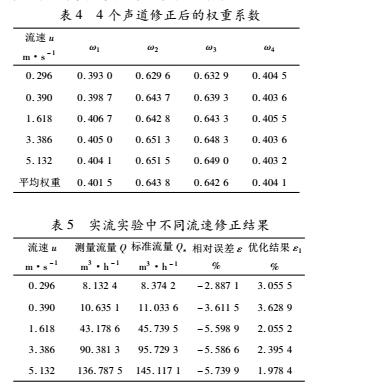
为获得优化后的权系数，对实际管路进行仿真。为保证仿真尽可能地符合实流实验，建立仿真模型与实流实验管路完全一致，如图 4 所示。按上述优化方法验证步骤对积分方法进行改进，从而获得入口速度为 0． 296、0． 390、1． 618、3． 386、5． 132m /s共 5 个流速点下的权重系数( 表4）。

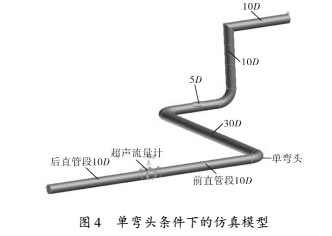
将得到的平均权重系数代入到实流实验数据中，验证其对实流实验的改进效果( 表 5) 。可以清晰地看出单弯头条件下优化前后的对比。在实流实验中，中高流速点处都有明显改善，优化后误差降低了 3． 60% 左右。分析小流量点处优化无明显改善的原因，认为积分方法改进是基于仿真数据优化权重系数，和实流实验之间存在一定的误差，在小流量点处，仿真和实流实验的误差较大，影响了实流实验最终优化的结果。

3.结论

3.1提出 Gauss-Jacobi 积分方案的优化方法。

基于 CFD 仿真方法，在表体段建立平行布置的199 条声道，提取各声道的线平均速度，用这些离散的速度值组成的集合来代替实际管路的流态分布; 计算各流速下的截面流动方程 F( t) ，进而求取新权重系数。

3.2单弯头理论模型的改进效果要明显优于实流实验改进的效果，对单弯头理论模型而言，优化后超声流量计测量误差绝对值均在 0． 06% 以内，精度提高了 0． 30% 。对实流实验来说，小流速点处修正前、后误差相近，中高流速点的误差降低了3． 60% 左右。