矿用高承压电磁流量计承压特性研究

随着煤矿开采逐渐向深部发展，电磁流量计安全应用于煤矿取决于其承压。研究了高承压电磁流量计的承压特性。建立了有限元仿真模型，对承压特性进行了仿真分析，得到了高承压电磁流量计的应力应变。为煤矿井下设备的承压特性研究提供了理论基础与分析方法。

1 .引言

随着浅部煤炭资源的日益枯竭，我国煤矿开采逐渐向深部发展，相继进入深部开采[1]。煤矿生产用水一般从地面通过管路系统从地面输送到工作面，那么大垂深产生的高静压对管路系统上的设备的承压提出了更高的要求。矿井降温工艺系统中的冷冻水和冷却水同样面临大垂深带来的高静压。因此，研究高承压、准确计量的矿用电磁流量计对矿井的安全、高效生产起到重要的作用[2]。

德国 EI 公司研制除了矿用本安型的电磁流量计，在国内唐山大方汇中仪表有限公司开发出了矿用隔爆型分体式电磁流量计。电磁流量计应用与煤矿除了解决防爆的问题，在高承压和井下复杂振动环境中，对其压力特性的研究也是重要的问题[3]。

2. 矿用高承压电磁流量计承压特性

2.1 电磁流量计原理

电磁流量计所依据的基本原理是法拉第电磁感应定律，

法拉第电磁感应定律是导体周围变动的磁场使导体中产生电动势[4]，如图 1 所示。

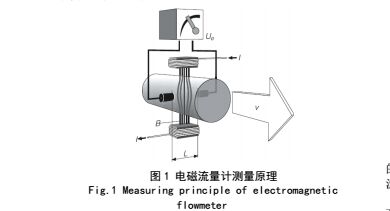
流体中产生的感应电动势被位于管子径向两端的一对电极拾取，该信号电压 Ue 与磁场强度 B、电极间距 L 和平均流速 V 成正比。而磁场强度 B 和电极距离 D 为常数，所以信号电压 Ue 与平均流速 V 成正比。

式中 Ue 为感应电压；B 为磁感应磁场；V 为液体流速；

为液体流量；A 为管道截面面积；L 为电极间距。

电磁流量计承压特性

处于井下高承压的电磁流量计，其承压特性主要取决于管腔所用的材料和尺寸结构。管腔中间可以看成一段柔性梁，取其中一段微元进行分析，如图 2 所示距中性层为 y0 处的纵向应变为

式中r 为距中性层为 y0 处曲率半径，Mz 为该截面的弯矩，E 为材料的杨氏模量，Iz 为横截面对 z 轴惯性矩，惯性矩为I   = bh 3 ，其中 l，b 和 h 分别为柔性梁的长、宽、高。

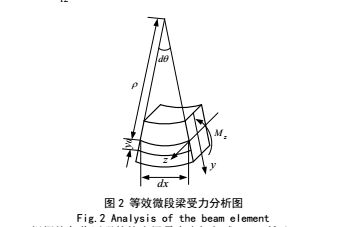
根据均匀收压强的简支梁最大弯矩如式（4）所示

式中 q 为这微端梁所受的均布载荷。综合式（3）与式（4）可以得到最大应变与承压的关系为

式中可以看出，电磁流量计管腔承压最大应变与其承受的压力呈线性关系，最大应变出现在管腔的中间，同时也是流量计的最大变形处。

矿用高承压电磁流量计的承压还与流量计的结构尺寸有关，主要的结构尺寸包括管径和壁厚。流量计的承压与其结构尺寸管径和壁厚的关系为

式中 P 为流量计承压，S 为流量计壁厚，D 为流量计管径；[s ] 为设计温度下材料许用应力，E 为调整系数。分析可知，流量计的承压与管径呈反比关系，与壁厚成正比关系。当壁厚一定时，流量计的承压随着管径的增大线性减小；当管径一定时，流量计的承压随着壁厚的增大而线性增大。

3 .有限元仿真与分析

3.1 ANSYS 建模

为了模拟矿用高承压电磁流量计的承压特性，以 DN200 的电磁流量计为例对其进行 ANSYS 仿真分析。电磁流量计的二维图如图 3 所示，结构尺寸如表 1 所示。为了方便建模，也为了更关注于流量计结构承压的部分，对其信号处理壳体及其他组成部分进行了简化，取其结构的一半进行建模。

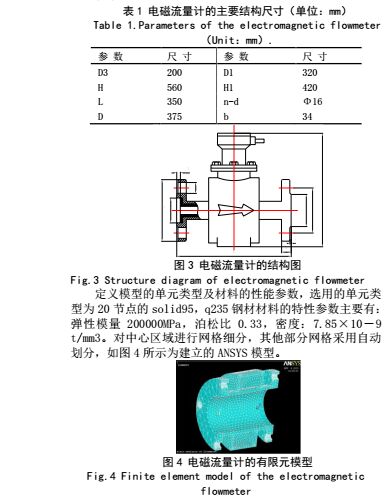
3.2 承压特性分析

模拟井下电磁流量计与地面垂直高差 1000 m，电磁流量计承受的静压为 10 MPa。在 ANSYS 模型基础上，对流量计法兰面的螺栓孔施加边界条件，对流量计的内表面施加10Mpa载荷，得到高承压电磁流量计von Mises等效应变，如图5所示。